Difference between revisions of "Irregularity"
From Encyclopedia of Mathematics
(Importing text file) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 13: | Line 13: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> R. Hartshorne, "Algebraic geometry" , Springer (1977) {{MR|0463157}} {{ZBL|0367.14001}} </TD></TR></table> |
Revision as of 21:53, 30 March 2012
A numerical invariant of a non-singular projective algebraic variety 
, equal to the dimension of its Picard variety. If the ground field has characteristic zero (or, more general, if the Picard scheme of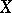 
is reduced), then the irregularity coincides with the dimension of the first cohomology space 
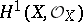with coefficients in the structure sheaf.
A variety with non-zero irregularity is called irregular, and a variety with zero irregularity — regular. Sometimes the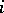 
-th irregularity of a complete linear system 
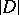on a variety 
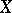is defined as
 |
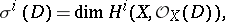where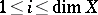 
.
Comments
References
| [a1] | R. Hartshorne, "Algebraic geometry" , Springer (1977) MR0463157 Zbl 0367.14001 |
How to Cite This Entry:
Irregularity. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Irregularity&oldid=23871
Irregularity. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Irregularity&oldid=23871
This article was adapted from an original article by I.V. Dolgachev (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article