Difference between revisions of "Extremal metric, method of the"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 5: | Line 5: | ||
The most important stages in the development of the method of the extremal metric were the introduction by L.V. Ahlfors and A. Beurling of the concept of the [[Extremal length|extremal length]] of a family of curves, the generalization proposed by J.A. Jenkins of the concept of the modulus of a family of curves to the case of several families of curves, and the proof of the uniqueness of the extremal metric in the moduli problem in this case. | The most important stages in the development of the method of the extremal metric were the introduction by L.V. Ahlfors and A. Beurling of the concept of the [[Extremal length|extremal length]] of a family of curves, the generalization proposed by J.A. Jenkins of the concept of the modulus of a family of curves to the case of several families of curves, and the proof of the uniqueness of the extremal metric in the moduli problem in this case. | ||
| − | Between 1939 and 1941 O. Teichmüller stated (without proof) a general principle asserting that the solutions of extremal problems in geometric function theory are connected in a definite way with certain quadratic differentials (cf. [[Quadratic differential|Quadratic differential]]). One of the most significant results in the development of the method of the extremal metric was Jenkins' | + | Between 1939 and 1941 O. Teichmüller stated (without proof) a general principle asserting that the solutions of extremal problems in geometric function theory are connected in a definite way with certain quadratic differentials (cf. [[Quadratic differential|Quadratic differential]]). One of the most significant results in the development of the method of the extremal metric was Jenkins' "general coefficient theorem" (see [[Jenkins theorem|Jenkins theorem]] and [[#References|[2]]]). This theorem contains as particular applications almost-all known elementary results concerning univalent functions (see, for example, [[Univalent function|Univalent function]]). The uniqueness result in Jenkins' theorem was sharpened and an analogue of this theorem was established for quadratic differentials without multiple poles (see ). In this way, certain extremal problems for domains with two and three distinguished boundary components were solved and the set of all extremal mappings was fully analyzed (see [[#References|[4]]] and [[#References|[5]]]). The solution of extremal problems by means of the "general coefficient theorem" is one of the forms of the method of the extremal metric and is much used in research. |
Another widely applied form of the method of the extremal metric is the version known as the moduli method. This technique is based on establishing a direct connection between a given extremal problem and a certain moduli problem for one or several families of curves (see [[Extremal length|Extremal length]] of a family of curves), and on solving this extremal-metric problem. As a rule, the extremal metric of the relevant moduli problem turns out to be a metric <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e037/e037180/e0371801.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e037/e037180/e0371802.png" /> is a quadratic differential the poles of which are determined from the conditions of the given problem. A direct examination of moduli problems for families of curves led to definite results in a number of questions related to the extremal partition of a given domain into a family of simply-connected and doubly-connected domains associated with specific homotopy classes of curves. The formulation of the latter goes back to the studies of M.A. Lavrent'ev and G.M. Goluzin (see [[#References|[5]]]). | Another widely applied form of the method of the extremal metric is the version known as the moduli method. This technique is based on establishing a direct connection between a given extremal problem and a certain moduli problem for one or several families of curves (see [[Extremal length|Extremal length]] of a family of curves), and on solving this extremal-metric problem. As a rule, the extremal metric of the relevant moduli problem turns out to be a metric <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e037/e037180/e0371801.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e037/e037180/e0371802.png" /> is a quadratic differential the poles of which are determined from the conditions of the given problem. A direct examination of moduli problems for families of curves led to definite results in a number of questions related to the extremal partition of a given domain into a family of simply-connected and doubly-connected domains associated with specific homotopy classes of curves. The formulation of the latter goes back to the studies of M.A. Lavrent'ev and G.M. Goluzin (see [[#References|[5]]]). | ||
| Line 11: | Line 11: | ||
The combination of the method of the extremal metric with variational methods and the [[Symmetrization method|symmetrization method]] has also been successful. Thus, the simultaneous use of the moduli method and the method of internal variations (cf. [[Internal variations, method of|Internal variations, method of]]) led to the proof of the existence of an extremal metric for the moduli problem for families of curves under very general assumptions. The combination of the method of the extremal metric and the method of symmetrization makes it possible in a number of cases to establish that the distribution of the poles of the associated quadratic differential has certain symmetry, and thus to reduce the given problem to a simpler case. | The combination of the method of the extremal metric with variational methods and the [[Symmetrization method|symmetrization method]] has also been successful. Thus, the simultaneous use of the moduli method and the method of internal variations (cf. [[Internal variations, method of|Internal variations, method of]]) led to the proof of the existence of an extremal metric for the moduli problem for families of curves under very general assumptions. The combination of the method of the extremal metric and the method of symmetrization makes it possible in a number of cases to establish that the distribution of the poles of the associated quadratic differential has certain symmetry, and thus to reduce the given problem to a simpler case. | ||
| − | There are also various other forms of the method of the extremal metric. One of them consists in solving extremal problems both for univalent and for multivalent mappings (in the latter case Teichmüller's principle is not applicable) by making direct use of the expressions for the areas of the images of some subsets of the given domain under the mapping in question, interpreted as the areas of the original sets in some new metric, in terms of the areas of the sets themselves. This form of the method of the extremal metric has turned out to be particularly effective in the solution of problems concerning the span of a multiply-connected domain (see [[#References|[7]]]). A development of this approach is Jenkins' | + | There are also various other forms of the method of the extremal metric. One of them consists in solving extremal problems both for univalent and for multivalent mappings (in the latter case Teichmüller's principle is not applicable) by making direct use of the expressions for the areas of the images of some subsets of the given domain under the mapping in question, interpreted as the areas of the original sets in some new metric, in terms of the areas of the sets themselves. This form of the method of the extremal metric has turned out to be particularly effective in the solution of problems concerning the span of a multiply-connected domain (see [[#References|[7]]]). A development of this approach is Jenkins' "special coefficient theorem" (see [[Jenkins theorem|Jenkins theorem]]). |
In a particular case this theorem reduces to the statement of the [[Area principle|area principle]]. | In a particular case this theorem reduces to the statement of the [[Area principle|area principle]]. | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> G.M. Goluzin, "Geometric theory of functions of a complex variable" , ''Transl. Math. Monogr.'' , '''26''' , Amer. Math. Soc. (1969) (Translated from Russian) {{MR|0247039}} {{ZBL|0183.07502}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> J.A. Jenkins, "Univalent functions and conformal mapping" , Springer (1958) {{MR|0096806}} {{ZBL|0083.29606}} </TD></TR><TR><TD valign="top">[3a]</TD> <TD valign="top"> P.M. Tamrazov, "Some extremal problems in conformal mapping" ''Math. USSR-Sb.'' , '''2''' : 1 (1967) pp. 85–109 ''Mat. Sb.'' , '''72''' : 1 (1967) pp. 59–71</TD></TR><TR><TD valign="top">[3b]</TD> <TD valign="top"> P.M. Tamrazov, "On the general coefficient theorem" ''Math. USSR-Sb.'' , '''1''' : 1 (1967) pp. 49–59 ''Mat. Sb.'' , '''73''' : 1 (1968) pp. 97–125 {{MR|0217284}} {{ZBL|0164.37902}} </TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> P.M. Tamrazov, "Supplement to the paper "Some extremal problems in conformal mapping" " ''Trudy Tomsk. Gos. Univ.'' , '''210''' : 6 (1969) pp. 111–118 (In Russian) {{MR|0283190}} {{ZBL|0221.30021}} </TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> G.V. Kuz'mina, "Moduli of families of curves and quadratic differentials" , Amer. Math. Soc. (1982) (Translated from Russian) {{MR|}} {{ZBL|0491.30013}} </TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> J.A. Jenkins, "On the existence of certain general extremal metrics" ''Ann. of Math.'' , '''66''' : 3 (1957) pp. 440–453 {{MR|0090648}} {{ZBL|0082.06301}} </TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> J.A. Jenkins, "On some span theorems" ''Illinois J. Math.'' , '''7''' : 1 (1963) pp. 104–117 {{MR|0150277}} {{ZBL|0112.05005}} </TD></TR><TR><TD valign="top">[8]</TD> <TD valign="top"> P.M. Tamrazov, "Theorems on covering of lines under conformal mapping" ''Mat. Sb.'' , '''66''' : 4 (1965) pp. 502–524 (In Russian) {{MR|178134}} {{ZBL|}} </TD></TR><TR><TD valign="top">[9]</TD> <TD valign="top"> A.V. Sychev, "Moduli and quasi-conformal mappings in space" , Novosibirsk (1983) (In Russian)</TD></TR><TR><TD valign="top">[10]</TD> <TD valign="top"> B. Rodin, "The method of extremal length" ''Bull. Amer. Math. Soc.'' , '''80''' : 4 (1974) pp. 587–606 {{MR|0361048}} {{ZBL|0286.30014}} </TD></TR></table> |
| Line 24: | Line 24: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> L.V. Ahlfors, "Conformal invariants. Topics in geometric function theory" , McGraw-Hill (1973) {{MR|0357743}} {{ZBL|0272.30012}} </TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> C. Pommerenke, "Univalent functions" , Vandenhoeck & Ruprecht (1975) {{MR|0507768}} {{ZBL|0298.30014}} </TD></TR></table> |
Revision as of 21:52, 30 March 2012
One of the fundamental methods in geometric function theory, closely connected with differential geometry and topology. The method of the extremal metric is based on the relations between the length of curves belonging to specific homotopy classes and the areas of the domains filled out by them. Here these curves and areas are computed in a special metric corresponding to the peculiarities of the extremal problem under investigation. (About extremal problems in geometric function theory see Univalent function.)
The method of the extremal metric has various forms. The original one is Grötzsch's strip method, which is an essential refinement of the arguments connecting length and area, operating with the characteristic conformal invariants of doubly-connected domains and quadrangles (see Grötzsch principle). Using his strip method, H. Grötzsch obtained a number of classical results in the theory of conformal and quasi-conformal mappings (see, for example, Grötzsch theorems).
The most important stages in the development of the method of the extremal metric were the introduction by L.V. Ahlfors and A. Beurling of the concept of the extremal length of a family of curves, the generalization proposed by J.A. Jenkins of the concept of the modulus of a family of curves to the case of several families of curves, and the proof of the uniqueness of the extremal metric in the moduli problem in this case.
Between 1939 and 1941 O. Teichmüller stated (without proof) a general principle asserting that the solutions of extremal problems in geometric function theory are connected in a definite way with certain quadratic differentials (cf. Quadratic differential). One of the most significant results in the development of the method of the extremal metric was Jenkins' "general coefficient theorem" (see Jenkins theorem and [2]). This theorem contains as particular applications almost-all known elementary results concerning univalent functions (see, for example, Univalent function). The uniqueness result in Jenkins' theorem was sharpened and an analogue of this theorem was established for quadratic differentials without multiple poles (see ). In this way, certain extremal problems for domains with two and three distinguished boundary components were solved and the set of all extremal mappings was fully analyzed (see [4] and [5]). The solution of extremal problems by means of the "general coefficient theorem" is one of the forms of the method of the extremal metric and is much used in research.
Another widely applied form of the method of the extremal metric is the version known as the moduli method. This technique is based on establishing a direct connection between a given extremal problem and a certain moduli problem for one or several families of curves (see Extremal length of a family of curves), and on solving this extremal-metric problem. As a rule, the extremal metric of the relevant moduli problem turns out to be a metric 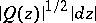 , where
, where 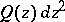 is a quadratic differential the poles of which are determined from the conditions of the given problem. A direct examination of moduli problems for families of curves led to definite results in a number of questions related to the extremal partition of a given domain into a family of simply-connected and doubly-connected domains associated with specific homotopy classes of curves. The formulation of the latter goes back to the studies of M.A. Lavrent'ev and G.M. Goluzin (see [5]).
is a quadratic differential the poles of which are determined from the conditions of the given problem. A direct examination of moduli problems for families of curves led to definite results in a number of questions related to the extremal partition of a given domain into a family of simply-connected and doubly-connected domains associated with specific homotopy classes of curves. The formulation of the latter goes back to the studies of M.A. Lavrent'ev and G.M. Goluzin (see [5]).
The combination of the method of the extremal metric with variational methods and the symmetrization method has also been successful. Thus, the simultaneous use of the moduli method and the method of internal variations (cf. Internal variations, method of) led to the proof of the existence of an extremal metric for the moduli problem for families of curves under very general assumptions. The combination of the method of the extremal metric and the method of symmetrization makes it possible in a number of cases to establish that the distribution of the poles of the associated quadratic differential has certain symmetry, and thus to reduce the given problem to a simpler case.
There are also various other forms of the method of the extremal metric. One of them consists in solving extremal problems both for univalent and for multivalent mappings (in the latter case Teichmüller's principle is not applicable) by making direct use of the expressions for the areas of the images of some subsets of the given domain under the mapping in question, interpreted as the areas of the original sets in some new metric, in terms of the areas of the sets themselves. This form of the method of the extremal metric has turned out to be particularly effective in the solution of problems concerning the span of a multiply-connected domain (see [7]). A development of this approach is Jenkins' "special coefficient theorem" (see Jenkins theorem).
In a particular case this theorem reduces to the statement of the area principle.
References
| [1] | G.M. Goluzin, "Geometric theory of functions of a complex variable" , Transl. Math. Monogr. , 26 , Amer. Math. Soc. (1969) (Translated from Russian) MR0247039 Zbl 0183.07502 |
| [2] | J.A. Jenkins, "Univalent functions and conformal mapping" , Springer (1958) MR0096806 Zbl 0083.29606 |
| [3a] | P.M. Tamrazov, "Some extremal problems in conformal mapping" Math. USSR-Sb. , 2 : 1 (1967) pp. 85–109 Mat. Sb. , 72 : 1 (1967) pp. 59–71 |
| [3b] | P.M. Tamrazov, "On the general coefficient theorem" Math. USSR-Sb. , 1 : 1 (1967) pp. 49–59 Mat. Sb. , 73 : 1 (1968) pp. 97–125 MR0217284 Zbl 0164.37902 |
| [4] | P.M. Tamrazov, "Supplement to the paper "Some extremal problems in conformal mapping" " Trudy Tomsk. Gos. Univ. , 210 : 6 (1969) pp. 111–118 (In Russian) MR0283190 Zbl 0221.30021 |
| [5] | G.V. Kuz'mina, "Moduli of families of curves and quadratic differentials" , Amer. Math. Soc. (1982) (Translated from Russian) Zbl 0491.30013 |
| [6] | J.A. Jenkins, "On the existence of certain general extremal metrics" Ann. of Math. , 66 : 3 (1957) pp. 440–453 MR0090648 Zbl 0082.06301 |
| [7] | J.A. Jenkins, "On some span theorems" Illinois J. Math. , 7 : 1 (1963) pp. 104–117 MR0150277 Zbl 0112.05005 |
| [8] | P.M. Tamrazov, "Theorems on covering of lines under conformal mapping" Mat. Sb. , 66 : 4 (1965) pp. 502–524 (In Russian) MR178134 |
| [9] | A.V. Sychev, "Moduli and quasi-conformal mappings in space" , Novosibirsk (1983) (In Russian) |
| [10] | B. Rodin, "The method of extremal length" Bull. Amer. Math. Soc. , 80 : 4 (1974) pp. 587–606 MR0361048 Zbl 0286.30014 |
Comments
References
| [a1] | L.V. Ahlfors, "Conformal invariants. Topics in geometric function theory" , McGraw-Hill (1973) MR0357743 Zbl 0272.30012 |
| [a2] | C. Pommerenke, "Univalent functions" , Vandenhoeck & Ruprecht (1975) MR0507768 Zbl 0298.30014 |
Extremal metric, method of the. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Extremal_metric,_method_of_the&oldid=23828