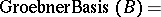Difference between revisions of "Buchberger algorithm"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 5: | Line 5: | ||
If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110980/b1109809.png" /> is a [[Field|field]], the algorithm also solves the following two problems: | If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110980/b1109809.png" /> is a [[Field|field]], the algorithm also solves the following two problems: | ||
| − | 2) Given a finite set of polynomial equations over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110980/b11098010.png" /> in the variables <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110980/b11098011.png" />, produce an | + | 2) Given a finite set of polynomial equations over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110980/b11098010.png" /> in the variables <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110980/b11098011.png" />, produce an "upper triangular form" of the equations, thus providing solutions by elimination of variables. |
3) Given a finite subset <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110980/b11098012.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110980/b11098013.png" />, produce an effectively computable <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110980/b11098014.png" />-linear projection mapping onto a complement in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110980/b11098015.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110980/b11098016.png" />, the ideal of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110980/b11098017.png" /> generated by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110980/b11098018.png" />. | 3) Given a finite subset <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110980/b11098012.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110980/b11098013.png" />, produce an effectively computable <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110980/b11098014.png" />-linear projection mapping onto a complement in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110980/b11098015.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110980/b11098016.png" />, the ideal of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110980/b11098017.png" /> generated by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110980/b11098018.png" />. | ||
| Line 43: | Line 43: | ||
while <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110980/b11098066.png" /> do | while <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110980/b11098066.png" /> do | ||
| − | + | choose <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110980/b11098067.png" />; | |
| − | + | <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110980/b11098068.png" />; | |
| − | + | <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110980/b11098069.png" />; | |
| − | + | if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110980/b11098070.png" /> then | |
| − | + | <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110980/b11098071.png" />; | |
| − | + | <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110980/b11098072.png" />; | |
| − | + | fi; | |
od; return <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110980/b11098073.png" />. | od; return <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110980/b11098073.png" />. | ||
| Line 76: | Line 76: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> W.W. Adam, P. Loustaunau, "An introduction to Gröbner bases" , ''Graduate Studies in Math.'' , '''3''' , Amer. Math. Soc. and Oxford Univ. Press (1994) {{MR|1287608}} {{ZBL|}} </TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> J. Apel, W. Lassner, "An extension of Buchberger's algorithm and calculations in enveloping fields of Lie algebras" ''J. Symb. Comp.'' , '''6''' (1988) pp. 361–370 {{MR|988423}} {{ZBL|}} </TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> B. Buchberger, "An algorithmic criterion for the solvability of algebraic systems of equations" ''Aequationes Math.'' , '''4''' (1965) pp. 374–383 (This paper is a published version of the author's Ph.D. Thesis (Innsbruck, 1965) under the advice of Prof. W. Gröbner)</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> B. Buchberger, "Gröbner bases: an algorithmic method in polynomial ideal theory" N.K. Bose (ed.) , ''Recent Trends in Multidimensional System Theory'' , Reidel (1985) pp. 184–232 {{MR|}} {{ZBL|0587.13009}} </TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> D. Cox, J. Little, D. O'Shea, "Ideals, varieties, and algorithms" , Springer (1992) {{MR|1189133}} {{ZBL|0756.13017}} </TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> D. Eisenbud, "Commutative algebra with a view toward algebraic geometry" , ''GTM'' , '''150''' , Springer (1995) {{MR|}} {{ZBL|0819.13001}} </TD></TR><TR><TD valign="top">[a7]</TD> <TD valign="top"> L. (ed.) Robbiano, "Computational aspects of commutative algebra" ''J. Symb. Comp.'' , '''special issue''' (1989) {{MR|1262830}} {{ZBL|0796.00017}} </TD></TR><TR><TD valign="top">[a8]</TD> <TD valign="top"> W. Trinks, "Über B. Buchbergers Verfahren, Systeme algebraischer Gleichungen zu lösen" ''J. Number Th.'' , '''10''' (1978) pp. 475–488 {{MR|0515056}} {{ZBL|0404.13004}} </TD></TR></table> |
Revision as of 21:50, 30 March 2012
A Noetherian ring  is called effective if its elements and ring operations can be described effectively as well as the problem of finding all solutions to a linear equation
is called effective if its elements and ring operations can be described effectively as well as the problem of finding all solutions to a linear equation  with
with  and unknown
and unknown  (in terms of a particular solution and a finite set of generators for the module of all homogeneous solutions). Examples are the rings of integers and of rational numbers, algebraic number fields, and finite rings. For such a ring
(in terms of a particular solution and a finite set of generators for the module of all homogeneous solutions). Examples are the rings of integers and of rational numbers, algebraic number fields, and finite rings. For such a ring  , the Buchberger algorithm (cf. [a3], [a4]) solves the following problem concerning the polynomial ring
, the Buchberger algorithm (cf. [a3], [a4]) solves the following problem concerning the polynomial ring  in the variables
in the variables  :
:
1) Provide algorithms turning  into an effective ring.
into an effective ring.
If  is a field, the algorithm also solves the following two problems:
is a field, the algorithm also solves the following two problems:
2) Given a finite set of polynomial equations over  in the variables
in the variables  , produce an "upper triangular form" of the equations, thus providing solutions by elimination of variables.
, produce an "upper triangular form" of the equations, thus providing solutions by elimination of variables.
3) Given a finite subset  of
of 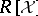 , produce an effectively computable
, produce an effectively computable 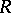 -linear projection mapping onto a complement in
-linear projection mapping onto a complement in 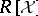 of
of 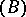 , the ideal of
, the ideal of 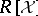 generated by
generated by  .
.
Monomials.
Denote by  the monoid of all monomials of
the monoid of all monomials of 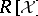 . For
. For  there is an
there is an 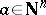 such that
such that  . A total order (cf. also Totally ordered set) on
. A total order (cf. also Totally ordered set) on  is called a reduction ordering if, for all
is called a reduction ordering if, for all  ,
,
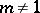 implies
implies  ;
;
 implies
implies  .
.
An important example is the lexicographical ordering (coming from the identification of  with
with 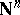 ). Starting from any reduction ordering
). Starting from any reduction ordering  and a vector
and a vector  , a new reduction ordering
, a new reduction ordering  can be obtained by demanding that
can be obtained by demanding that  if and only if either
if and only if either 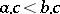 or
or  and
and  . If
. If  is the all-one vector, the order refines the partial order by total degree.
is the all-one vector, the order refines the partial order by total degree.
Termination of the Buchberger algorithm follows from the fact that a reduction ordering on  is well founded.
is well founded.
These orderings are used to compare (sets of) polynomials. To single out the highest monomial and coefficient from a non-zero polynomial 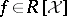 , set
, set
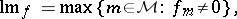 |
 |
The letters 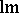 ,
,  ,
,  stand for leading monomial, leading coefficient and leading term, respectively.
stand for leading monomial, leading coefficient and leading term, respectively.
The Buchberger algorithm in its simplest form.
Let  be a field and
be a field and  a finite subset of
a finite subset of  . Let
. Let  denote a remainder of
denote a remainder of 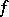 with respect to
with respect to  , that is, the result of iteratively replacing
, that is, the result of iteratively replacing  by a polynomial of the form
by a polynomial of the form  with
with 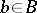 such that
such that  as often as possible. This is effective because
as often as possible. This is effective because  is well founded. The result is not uniquely determined by
is well founded. The result is not uniquely determined by  . Given
. Given 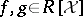 , their
, their  -polynomial is
-polynomial is
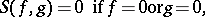 |
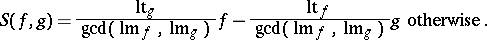 |
The following routine is the Buchberger algorithm in its simplest form.
;
whiledo
choose;
;
;
ifthen
;
;
fi;
od; return.
It terminates because the sequence of consecutive sets  , produced in the course of the algorithm, descends with respect to
, produced in the course of the algorithm, descends with respect to  .
.
Note that 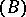 is an invariant of the algorithm. Consequently, if
is an invariant of the algorithm. Consequently, if  is the output resulting from input
is the output resulting from input  , then
, then  . The output
. The output  has the following characteristic property:
has the following characteristic property:
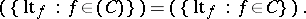 |
A subset 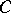 of
of  with this property is called a Gröbner basis. Equivalently, a subset
with this property is called a Gröbner basis. Equivalently, a subset  of
of 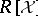 is a Gröbner basis if and only if, for all
is a Gröbner basis if and only if, for all  , one has
, one has  .
.
Suppose that 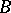 is a Gröbner basis. Then
is a Gröbner basis. Then 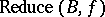 is uniquely determined for each
is uniquely determined for each  . A monomial is called standard with respect to an ideal
. A monomial is called standard with respect to an ideal  if it is not of the form
if it is not of the form  for some
for some  . The mapping
. The mapping  is an effectively computable projection onto the
is an effectively computable projection onto the  -span of all standard monomials with respect to
-span of all standard monomials with respect to 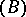 , which is a complement as in Problem 3) above.
, which is a complement as in Problem 3) above.
A reduction ordering 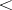 with
with  is called an elimination ordering if
is called an elimination ordering if 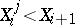 for
for  and
and  . If
. If  is a Gröbner basis with respect to an elimination ordering, then
is a Gröbner basis with respect to an elimination ordering, then 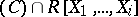 is the ideal of
is the ideal of  generated by
generated by  . This is the key to solving Problem 2.
. This is the key to solving Problem 2.
The Buchberger algorithm can be generalized to arbitrary effective rings  . By keeping track of intermediate results in the algorithms, it is possible to express the Gröbner basis
. By keeping track of intermediate results in the algorithms, it is possible to express the Gröbner basis  coming from input
coming from input 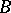 as an
as an 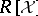 -linear combination of
-linear combination of  . Using this, one can find a particular solution, as well as a finite generating set for all homogeneous solutions to an
. Using this, one can find a particular solution, as well as a finite generating set for all homogeneous solutions to an  -linear equation, and hence a solution to Problem 1.
-linear equation, and hence a solution to Problem 1.
General introductions to the Buchberger algorithm can be found in [a1], [a5], [a6]. More advanced applications can be found in [a7], which also contains an indication of the badness of the complexity of finding Gröbner bases. Buchberger algorithms over more general coefficient domains 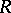 are dealt with in [a8], and generalizations from
are dealt with in [a8], and generalizations from 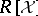 to particular non-commutative algebras (e.g., the universal enveloping algebra of a Lie algebra) in [a2].
to particular non-commutative algebras (e.g., the universal enveloping algebra of a Lie algebra) in [a2].
References
| [a1] | W.W. Adam, P. Loustaunau, "An introduction to Gröbner bases" , Graduate Studies in Math. , 3 , Amer. Math. Soc. and Oxford Univ. Press (1994) MR1287608 |
| [a2] | J. Apel, W. Lassner, "An extension of Buchberger's algorithm and calculations in enveloping fields of Lie algebras" J. Symb. Comp. , 6 (1988) pp. 361–370 MR988423 |
| [a3] | B. Buchberger, "An algorithmic criterion for the solvability of algebraic systems of equations" Aequationes Math. , 4 (1965) pp. 374–383 (This paper is a published version of the author's Ph.D. Thesis (Innsbruck, 1965) under the advice of Prof. W. Gröbner) |
| [a4] | B. Buchberger, "Gröbner bases: an algorithmic method in polynomial ideal theory" N.K. Bose (ed.) , Recent Trends in Multidimensional System Theory , Reidel (1985) pp. 184–232 Zbl 0587.13009 |
| [a5] | D. Cox, J. Little, D. O'Shea, "Ideals, varieties, and algorithms" , Springer (1992) MR1189133 Zbl 0756.13017 |
| [a6] | D. Eisenbud, "Commutative algebra with a view toward algebraic geometry" , GTM , 150 , Springer (1995) Zbl 0819.13001 |
| [a7] | L. (ed.) Robbiano, "Computational aspects of commutative algebra" J. Symb. Comp. , special issue (1989) MR1262830 Zbl 0796.00017 |
| [a8] | W. Trinks, "Über B. Buchbergers Verfahren, Systeme algebraischer Gleichungen zu lösen" J. Number Th. , 10 (1978) pp. 475–488 MR0515056 Zbl 0404.13004 |
Buchberger algorithm. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Buchberger_algorithm&oldid=23773