Difference between revisions of "Median (in statistics)"
(MSC|60-01|62-01) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 4: | Line 4: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> M. Loève, "Probability theory" , Springer (1977) {{MR|0651017}} {{MR|0651018}} {{ZBL|0359.60001}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> H. Cramér, "Mathematical methods of statistics" , Princeton Univ. Press (1946) {{MR|0016588}} {{ZBL|0063.01014}} </TD></TR></table> |
Revision as of 10:31, 27 March 2012
2020 Mathematics Subject Classification: Primary: 60-01 Secondary: 62-01 [MSN][ZBL]
One of the numerical characteristics of probability distributions, a particular case of a quantile. For a real-valued random variable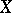 
with distribution function 
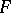, a median is defined as a number 
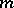such that 
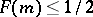and 
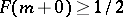. Every random variable has at least one median. If 
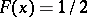for all 
in a closed interval, then every point of this interval is a median. If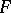 
is a strictly-monotone function, then the median is unique. In the symmetric case, if the median is unique, it is identical with the mathematical expectation, provided that the latter exists. The fact that a median always exists is used for centering random variables (see, for instance, Lévy inequality). In mathematical statistics, to estimate the median of a distribution in terms of independent results of observations 
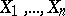one uses a so-called sample median — a median of the corresponding order statistics (cf. Order statistic) 
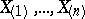, that is, of the quantity 
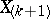if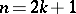 
is odd, and of 
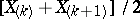if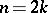 
is even.
References
| [1] | M. Loève, "Probability theory" , Springer (1977) MR0651017 MR0651018 Zbl 0359.60001 |
| [2] | H. Cramér, "Mathematical methods of statistics" , Princeton Univ. Press (1946) MR0016588 Zbl 0063.01014 |
Median (in statistics). Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Median_(in_statistics)&oldid=23634