Difference between revisions of "Mathematical expectation"
(MSC|60-01) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 53: | Line 53: | ||
The mathematical expectation is used to define many numerical functional characteristics of probability distributions (as the mathematical expectations of appropriate functions in the given random variables), for example, the [[Generating function|generating function]], the [[Characteristic function|characteristic function]] and the moments (cf. [[Moment|Moment]]) of all orders, in particular, the variance (cf. [[Dispersion|Dispersion]]) and the [[Covariance|covariance]]. | The mathematical expectation is used to define many numerical functional characteristics of probability distributions (as the mathematical expectations of appropriate functions in the given random variables), for example, the [[Generating function|generating function]], the [[Characteristic function|characteristic function]] and the moments (cf. [[Moment|Moment]]) of all orders, in particular, the variance (cf. [[Dispersion|Dispersion]]) and the [[Covariance|covariance]]. | ||
| − | The mathematical expectation is a characteristic of the location of the values of a random variable (the mean value of its distribution). Here, the mathematical expectation serves as a | + | The mathematical expectation is a characteristic of the location of the values of a random variable (the mean value of its distribution). Here, the mathematical expectation serves as a "typical" value from the distribution and its role is analogous to the role played in mechanics by the statical momentum — the coordinates of the barycentre of a mass distribution. The mathematical expectation differs from other characteristics of location which describe the distribution in general terms — like the median (cf. [[Median (in statistics)|Median (in statistics)]]) and the [[Mode|mode]], by the higher importance that it and its corresponding scatter characteristic, the variance, have in limit theorems of probability theory. The meaning of the mathematical expectation is most completely revealed by the [[Law of large numbers|law of large numbers]] (see also [[Chebyshev inequality in probability theory|Chebyshev inequality in probability theory]]) and the [[Strong law of large numbers|strong law of large numbers]]. In particular, if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m062/m062630/m06263045.png" /> is a sequence of mutually-independent identically-distributed random variables with finite mathematical expectation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m062/m062630/m06263046.png" />, then, as <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m062/m062630/m06263047.png" /> and for every <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m062/m062630/m06263048.png" />, |
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m062/m062630/m06263049.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m062/m062630/m06263049.png" /></td> </tr></table> | ||
| Line 63: | Line 63: | ||
with probability one. | with probability one. | ||
| − | The notion of the mathematical expectation as the expected value of a random variable was first noticed in the 18th century in connection with the theory of games of chance. Initially the term | + | The notion of the mathematical expectation as the expected value of a random variable was first noticed in the 18th century in connection with the theory of games of chance. Initially the term "mathematical expectation" was introduced as the expected pay-off of a player, equal to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m062/m062630/m06263051.png" /> for possible pay-offs <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m062/m062630/m06263052.png" /> with respective probabilities <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m062/m062630/m06263053.png" />. Primary contributions in the generalization and utilization of the notion of the mathematical expectation in its contemporary meaning are due to P.L. Chebyshev. |
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> A.N. Kolmogorov, "Foundations of the theory of probability" , Chelsea, reprint (1950) (Translated from Russian) {{MR|0032961}} {{ZBL|}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> W. Feller, "An introduction to probability theory and its applications" , '''1–2''' , Wiley (1957–1971) {{MR|0779091}} {{MR|0779090}} {{MR|0270403}} {{MR|0228020}} {{MR|1534302}} {{MR|0243559}} {{MR|0242202}} {{MR|0210154}} {{MR|1570945}} {{MR|0088081}} {{MR|1528130}} {{MR|0067380}} {{MR|0038583}} {{ZBL|0598.60003}} {{ZBL|0598.60002}} {{ZBL|0219.60003}} {{ZBL|0155.23101}} {{ZBL|0158.34902}} {{ZBL|0151.22403}} {{ZBL|0138.10207}} {{ZBL|0115.35308}} {{ZBL|0077.12201}} {{ZBL|0039.13201}} </TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> M. Loève, "Probability theory" , Springer (1978) {{MR|0651017}} {{MR|0651018}} {{ZBL|0385.60001}} </TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> H. Cramér, "Mathematical methods of statistics" , Princeton Univ. Press (1946) {{MR|0016588}} {{ZBL|0063.01014}} </TD></TR></table> |
Revision as of 10:31, 27 March 2012
mean value, of a random variable
2020 Mathematics Subject Classification: Primary: 60-01 [MSN][ZBL]
A numerical characteristic of the probability distribution of a random variable. In the most general setting, the mathematical expectation of a random variable 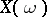 ,
, 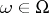 , is defined as the Lebesgue integral with respect to a probability measure
, is defined as the Lebesgue integral with respect to a probability measure 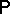 on a given probability space
on a given probability space 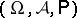 :
:
 | (*) |
provided the integral exists. The mathematical expectation of a real-valued random variable may be calculated also as the Lebesgue integral of  with respect to the probability distribution
with respect to the probability distribution 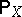 of
of 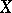 :
:
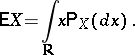 |
The mathematical expectation of a function in 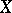 is expressible in terms of the distribution
is expressible in terms of the distribution 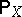 ; for example, if
; for example, if 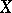 is a random variable with values in
is a random variable with values in 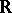 and
and 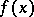 is a single-valued Borel function of
is a single-valued Borel function of  , then
, then
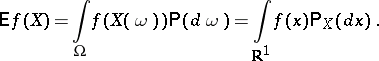 |
If 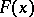 is the distribution function of
is the distribution function of 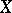 , then the mathematical expectation of
, then the mathematical expectation of 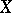 can be represented as the Lebesgue–Stieltjes (or Riemann–Stieltjes) integral
can be represented as the Lebesgue–Stieltjes (or Riemann–Stieltjes) integral
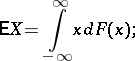 |
here integrability of 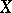 in the sense of (*) is equivalent to the finiteness of the integral
in the sense of (*) is equivalent to the finiteness of the integral
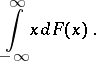 |
In particular cases, if 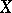 has a discrete distribution with possible values
has a discrete distribution with possible values 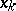 ,
, 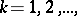 and corresponding probabilities
and corresponding probabilities 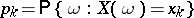 , then
, then
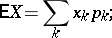 |
if 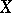 has an absolutely continuous distribution with probability density
has an absolutely continuous distribution with probability density 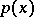 , then
, then
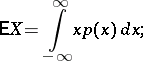 |
moreover, the existence of the mathematical expectation is equivalent to the absolute convergence of the corresponding series or integral.
Main properties of the mathematical expectation:
a) 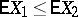 whenever
whenever 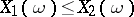 for all
for all 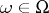 ;
;
b) 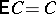 for every real constant
for every real constant 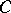 ;
;
c) 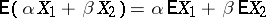 for all real
for all real 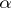 and
and 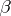 ;
;
d) 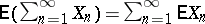 if the series
if the series 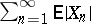 converges;
converges;
e) 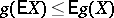 for convex functions
for convex functions 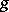 ;
;
f) every bounded random variable has a finite mathematical expectation;
g) 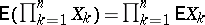 if the random variables
if the random variables 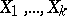 are mutually independent.
are mutually independent.
One can naturally define the notion of a random variable with an infinite mathematical expectation. A typical example is provided by the return times in certain random walks (see, e.g., Bernoulli random walk).
The mathematical expectation is used to define many numerical functional characteristics of probability distributions (as the mathematical expectations of appropriate functions in the given random variables), for example, the generating function, the characteristic function and the moments (cf. Moment) of all orders, in particular, the variance (cf. Dispersion) and the covariance.
The mathematical expectation is a characteristic of the location of the values of a random variable (the mean value of its distribution). Here, the mathematical expectation serves as a "typical" value from the distribution and its role is analogous to the role played in mechanics by the statical momentum — the coordinates of the barycentre of a mass distribution. The mathematical expectation differs from other characteristics of location which describe the distribution in general terms — like the median (cf. Median (in statistics)) and the mode, by the higher importance that it and its corresponding scatter characteristic, the variance, have in limit theorems of probability theory. The meaning of the mathematical expectation is most completely revealed by the law of large numbers (see also Chebyshev inequality in probability theory) and the strong law of large numbers. In particular, if 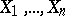 is a sequence of mutually-independent identically-distributed random variables with finite mathematical expectation
is a sequence of mutually-independent identically-distributed random variables with finite mathematical expectation 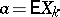 , then, as
, then, as 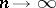 and for every
and for every 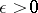 ,
,
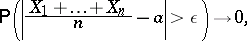 |
and, in addition,
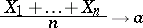 |
with probability one.
The notion of the mathematical expectation as the expected value of a random variable was first noticed in the 18th century in connection with the theory of games of chance. Initially the term "mathematical expectation" was introduced as the expected pay-off of a player, equal to 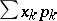 for possible pay-offs
for possible pay-offs  with respective probabilities
with respective probabilities  . Primary contributions in the generalization and utilization of the notion of the mathematical expectation in its contemporary meaning are due to P.L. Chebyshev.
. Primary contributions in the generalization and utilization of the notion of the mathematical expectation in its contemporary meaning are due to P.L. Chebyshev.
References
| [1] | A.N. Kolmogorov, "Foundations of the theory of probability" , Chelsea, reprint (1950) (Translated from Russian) MR0032961 |
| [2] | W. Feller, "An introduction to probability theory and its applications" , 1–2 , Wiley (1957–1971) MR0779091 MR0779090 MR0270403 MR0228020 MR1534302 MR0243559 MR0242202 MR0210154 MR1570945 MR0088081 MR1528130 MR0067380 MR0038583 Zbl 0598.60003 Zbl 0598.60002 Zbl 0219.60003 Zbl 0155.23101 Zbl 0158.34902 Zbl 0151.22403 Zbl 0138.10207 Zbl 0115.35308 Zbl 0077.12201 Zbl 0039.13201 |
| [3] | M. Loève, "Probability theory" , Springer (1978) MR0651017 MR0651018 Zbl 0385.60001 |
| [4] | H. Cramér, "Mathematical methods of statistics" , Princeton Univ. Press (1946) MR0016588 Zbl 0063.01014 |
Mathematical expectation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Mathematical_expectation&oldid=23630