Difference between revisions of "Cramér theorem"
Ulf Rehmann (talk | contribs) m (moved Cramer theorem to Cramér theorem over redirect: accented title) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 16: | Line 16: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> H. Cramér, "Sur un nouveau théorème-limite de la théorie des probabilités" , ''Act. Sci. et Ind.'' , '''736''' , Hermann (1938) {{MR|}} {{ZBL|64.0529.01}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> I.A. Ibragimov, Yu.V. Linnik, "Independent and stationary sequences of random variables" , Wolters-Noordhoff (1971) (Translated from Russian) {{MR|0322926}} {{ZBL|0219.60027}} </TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> V.V. Petrov, "Sums of independent random variables" , Springer (1975) (Translated from Russian) {{MR|0388499}} {{ZBL|0322.60043}} {{ZBL|0322.60042}} </TD></TR></table> |
| Line 24: | Line 24: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> R.S. Ellis, "Entropy, large deviations, and statistical mechanics" , Springer (1985) {{MR|0793553}} {{ZBL|0566.60097}} </TD></TR></table> |
Revision as of 10:30, 27 March 2012
2020 Mathematics Subject Classification: Primary: 60F10 [MSN][ZBL]
An integral limit theorem for the probability of large deviations of sums of independent random variables. Let 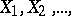 be a sequence of independent random variables with the same non-degenerate distribution function
be a sequence of independent random variables with the same non-degenerate distribution function 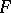 , such that
, such that 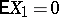 and such that the generating function
and such that the generating function 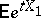 of the moments is finite in some interval
of the moments is finite in some interval 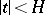 (this last condition is known as the Cramér condition). Let
(this last condition is known as the Cramér condition). Let
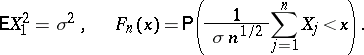 |
If 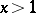 ,
,  as
as 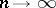 , then
, then
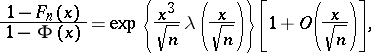 |
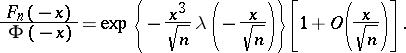 |
Here 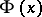 is the normal
is the normal  distribution function and
distribution function and 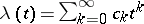 is the so-called Cramér series, the coefficients of which depend only on the moments of the random variable
is the so-called Cramér series, the coefficients of which depend only on the moments of the random variable 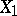 ; this series is convergent for all sufficiently small
; this series is convergent for all sufficiently small 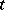 . Actually, the original result, obtained by H. Cramér in 1938, was somewhat weaker than that just described.
. Actually, the original result, obtained by H. Cramér in 1938, was somewhat weaker than that just described.
References
| [1] | H. Cramér, "Sur un nouveau théorème-limite de la théorie des probabilités" , Act. Sci. et Ind. , 736 , Hermann (1938) Zbl 64.0529.01 |
| [2] | I.A. Ibragimov, Yu.V. Linnik, "Independent and stationary sequences of random variables" , Wolters-Noordhoff (1971) (Translated from Russian) MR0322926 Zbl 0219.60027 |
| [3] | V.V. Petrov, "Sums of independent random variables" , Springer (1975) (Translated from Russian) MR0388499 Zbl 0322.60043 Zbl 0322.60042 |
Comments
See also Limit theorems; Probability of large deviations.
References
| [a1] | R.S. Ellis, "Entropy, large deviations, and statistical mechanics" , Springer (1985) MR0793553 Zbl 0566.60097 |
Cramér theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Cram%C3%A9r_theorem&oldid=23599