Difference between revisions of "Branching process with immigration"
(MSC|60J80 Category:Branching processes) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 3: | Line 3: | ||
[[Category:Branching processes]] | [[Category:Branching processes]] | ||
| − | A model of a branching process (discrete-time or continuous-time, with one or several types of particles, etc.) in which new particles may appear not only as the products of division of the original particles, but also as a result of immigration from some | + | A model of a branching process (discrete-time or continuous-time, with one or several types of particles, etc.) in which new particles may appear not only as the products of division of the original particles, but also as a result of immigration from some "external source" . For instance, let |
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b017/b017580/b0175801.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b017/b017580/b0175801.png" /></td> </tr></table> | ||
| Line 54: | Line 54: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> A.M. Zubkov, "Life-like periods of a branching process with immigration" ''Theory Probab. Appl.'' , '''17''' : 1 (1972) pp. 174–183 ''Teor. Veroyatnost. i Primenen.'' , '''17''' : 1 (1972) pp. 179–188</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> A.G. Pakes, "Further results on the critical Galton–Watson process with immigration" ''J. Austral. Math. Soc.'' , '''13''' : 3 (1972) pp. 277–290 {{MR|0312585}} {{ZBL|0235.60078}} </TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> J.H. Foster, J.A. Williamson, "Limit theorems for the Galton–Watson process with time-dependent immigration" ''Z. Wahrsch. Verw. Geb.'' , '''20''' (1971) pp. 227–235 {{MR|0305494}} {{ZBL|0219.60069}} {{ZBL|0212.19702}} </TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> E. Seneta, "An explicit limit theorem for the critical Galton–Watson process with immigration" ''J. Roy. Statist. Soc. Ser. B'' , '''32''' : 1 (1970) pp. 149–152 {{MR|0266320}} {{ZBL|0198.52002}} </TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> E. Seneta, "On the supercritical Galton–Watson process with immigration" ''Math. Biosci.'' , '''7''' (1970) pp. 9–14 {{MR|0270460}} {{MR|0268974}} {{ZBL|0209.48804}} </TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> J.H. Foster, "A limit theorem for a branching process with state-dependent immigration" ''Ann. of Math. Statist.'' , '''42''' : 5 (1971) pp. 1773–1776 {{MR|0348854}} {{ZBL|0245.60063}} </TD></TR></table> |
Revision as of 10:30, 27 March 2012
2020 Mathematics Subject Classification: Primary: 60J80 [MSN][ZBL]
A model of a branching process (discrete-time or continuous-time, with one or several types of particles, etc.) in which new particles may appear not only as the products of division of the original particles, but also as a result of immigration from some "external source" . For instance, let
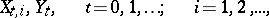 |
be independent random variables with generating functions
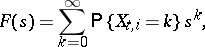 |
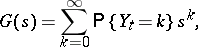 |
respectively; the branching Galton–Watson process with immigration may be defined by the relations 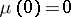 , where
, where 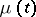 is the number of particles and
is the number of particles and
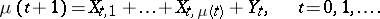 |
Here, the variable 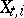 is interpreted as the number of daughter particles of the
is interpreted as the number of daughter particles of the 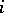 -th particle of the
-th particle of the 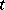 -th generation, while the variable
-th generation, while the variable 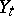 is interpreted as the number of the particles which have immigrated into the
is interpreted as the number of the particles which have immigrated into the 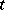 -th generation. The generating functions
-th generation. The generating functions
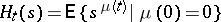 |
are given by the recurrence relations
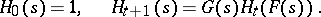 |
The Markov chain 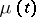 corresponding to the Galton–Watson branching process with immigration is recurrent if
corresponding to the Galton–Watson branching process with immigration is recurrent if 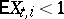 and
and 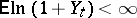 or
or 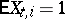 and
and 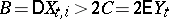 , and is transient if
, and is transient if 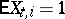 and
and 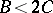 or
or 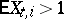 . For the Markov chain
. For the Markov chain 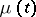 to be ergodic, i.e. for the limits
to be ergodic, i.e. for the limits
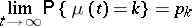 |
to exist and to satisfy
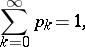 |
it is necessary and sufficient [3] that
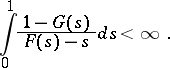 |
This condition is met, in particular, if 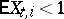 and
and 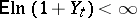 . If
. If 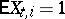 ,
, 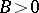 ,
, 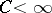 , then [4]
, then [4]
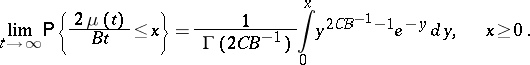 |
If 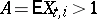 and
and 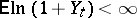 , then there exists [5] a sequence of numbers
, then there exists [5] a sequence of numbers 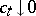 ,
, 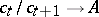 , such that
, such that
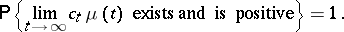 |
In branching processes with immigration in which the immigration takes place at 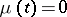 only, i.e.
only, i.e.
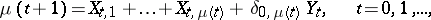 |
where  is the Kronecker symbol, the following relation is valid if
is the Kronecker symbol, the following relation is valid if 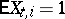 ,
, 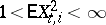 and
and 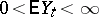 :
:
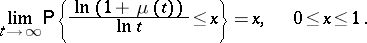 |
References
| [1] | A.M. Zubkov, "Life-like periods of a branching process with immigration" Theory Probab. Appl. , 17 : 1 (1972) pp. 174–183 Teor. Veroyatnost. i Primenen. , 17 : 1 (1972) pp. 179–188 |
| [2] | A.G. Pakes, "Further results on the critical Galton–Watson process with immigration" J. Austral. Math. Soc. , 13 : 3 (1972) pp. 277–290 MR0312585 Zbl 0235.60078 |
| [3] | J.H. Foster, J.A. Williamson, "Limit theorems for the Galton–Watson process with time-dependent immigration" Z. Wahrsch. Verw. Geb. , 20 (1971) pp. 227–235 MR0305494 Zbl 0219.60069 Zbl 0212.19702 |
| [4] | E. Seneta, "An explicit limit theorem for the critical Galton–Watson process with immigration" J. Roy. Statist. Soc. Ser. B , 32 : 1 (1970) pp. 149–152 MR0266320 Zbl 0198.52002 |
| [5] | E. Seneta, "On the supercritical Galton–Watson process with immigration" Math. Biosci. , 7 (1970) pp. 9–14 MR0270460 MR0268974 Zbl 0209.48804 |
| [6] | J.H. Foster, "A limit theorem for a branching process with state-dependent immigration" Ann. of Math. Statist. , 42 : 5 (1971) pp. 1773–1776 MR0348854 Zbl 0245.60063 |
Comments
Additional references may be found in the article Branching process.
Branching process with immigration. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Branching_process_with_immigration&oldid=23588