Difference between revisions of "Borel measure"
(better MSC template) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 24: | Line 24: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> V.S. Varadarajan, "Measures on topological spaces" ''Transl. Amer. Math. Soc. Ser. 2'' , '''48''' (1965) pp. 161–228 ''Mat. Sb.'' , '''55 (97)''' : 1 (1961) pp. 35–100 {{MR|0148838}} {{ZBL|}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> P.R. Halmos, "Measure theory" , v. Nostrand (1950) {{MR|0033869}} {{ZBL|0040.16802}} </TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> J. Neveu, "Bases mathématiques du calcul des probabilités" , Masson (1970) {{MR|0272004}} {{ZBL|0203.49901}} </TD></TR></table> |
| Line 32: | Line 32: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> H.L. Royden, "Real analysis" , Macmillan (1968) {{MR|1013117}} {{MR|1532990}} {{MR|0151555}} {{ZBL|1191.26002}} {{ZBL|0704.26006}} {{ZBL|0197.03501}} {{ZBL|0121.05501}} </TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> A.C. Zaanen, "Integration" , North-Holland (1967) {{MR|0222234}} {{ZBL|0175.05002}} </TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> W. Rudin, "Principles of mathematical analysis" , McGraw-Hill (1953) {{MR|0055409}} {{ZBL|0052.05301}} </TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> W. Rudin, "Real and complex analysis" , McGraw-Hill (1966) pp. 98 {{MR|0210528}} {{ZBL|0142.01701}} </TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> A.E. Taylor, "General theory of functions and integration" , Blaisdell (1965) {{MR|0178100}} {{ZBL|0135.11301}} </TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> C.D. Aliprantz, O. Burleinshaw, "Principles of real analysis" , North-Holland (1981)</TD></TR></table> |
Revision as of 10:29, 27 March 2012
of sets
2020 Mathematics Subject Classification: Primary: 28C15 [MSN][ZBL]
A non-negative function 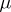 of the subsets of a topological space
of the subsets of a topological space 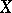 possessing the following properties: 1) its domain of definition is the
possessing the following properties: 1) its domain of definition is the 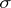 -algebra
-algebra 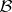 of Borel sets (cf. Borel set) in
of Borel sets (cf. Borel set) in 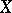 , i.e. the smallest class of subsets in
, i.e. the smallest class of subsets in 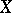 containing the open sets and closed with respect to the set-theoretic operations performed a countable number of times; and 2)
containing the open sets and closed with respect to the set-theoretic operations performed a countable number of times; and 2)  if
if 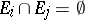 when
when 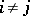 , i.e.
, i.e. 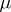 is countably additive. A Borel measure
is countably additive. A Borel measure 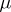 is called regular if
is called regular if
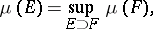 |
where 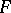 belongs to the class
belongs to the class 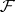 of closed subsets in
of closed subsets in  . The study of Borel measures is often connected with that of Baire measures, which differ from Borel measures only in their domain of definition: They are defined on the smallest
. The study of Borel measures is often connected with that of Baire measures, which differ from Borel measures only in their domain of definition: They are defined on the smallest 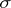 -algebra
-algebra 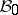 with respect to which all continuous functions on
with respect to which all continuous functions on 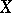 are measurable. A Borel measure
are measurable. A Borel measure 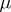 (or a Baire measure
(or a Baire measure  ) is said to be
) is said to be  -smooth if
-smooth if  for any net
for any net 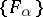 of closed sets which satisfies the condition
of closed sets which satisfies the condition 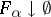 (or
(or 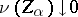 for any net
for any net 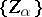 of sets which are zero sets of continuous functions and such that
of sets which are zero sets of continuous functions and such that 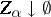 ). A Borel measure
). A Borel measure  (or Baire measure
(or Baire measure  ) is said to be tight if
) is said to be tight if
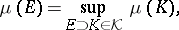 |
where 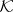 is the class of compact subsets on
is the class of compact subsets on 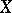 (or
(or
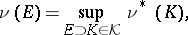 |
where
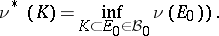 |
Tightness and  -smoothness are restrictions which ensure additional smoothness of measures, and which in fact often hold. Under certain conditions Baire measures can be extended to Borel measures. For instance, if
-smoothness are restrictions which ensure additional smoothness of measures, and which in fact often hold. Under certain conditions Baire measures can be extended to Borel measures. For instance, if 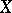 is a completely-regular Hausdorff space, then any
is a completely-regular Hausdorff space, then any  -smooth (tight) finite Baire measure can be extended to a regular
-smooth (tight) finite Baire measure can be extended to a regular  -smooth (tight) finite Borel measure. In the study of measures on locally compact spaces Borel measures (or Baire measures) is the name sometimes given to measures defined on the
-smooth (tight) finite Borel measure. In the study of measures on locally compact spaces Borel measures (or Baire measures) is the name sometimes given to measures defined on the 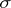 -ring of sets generated by the compact (or
-ring of sets generated by the compact (or 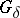 -compact) sets and which are finite on compact sets. Often, by the Borel measure on the real line one understands the measure defined on the Borel sets such that its value on an arbitrary segment is equal to the length of that segment.
-compact) sets and which are finite on compact sets. Often, by the Borel measure on the real line one understands the measure defined on the Borel sets such that its value on an arbitrary segment is equal to the length of that segment.
References
| [1] | V.S. Varadarajan, "Measures on topological spaces" Transl. Amer. Math. Soc. Ser. 2 , 48 (1965) pp. 161–228 Mat. Sb. , 55 (97) : 1 (1961) pp. 35–100 MR0148838 |
| [2] | P.R. Halmos, "Measure theory" , v. Nostrand (1950) MR0033869 Zbl 0040.16802 |
| [3] | J. Neveu, "Bases mathématiques du calcul des probabilités" , Masson (1970) MR0272004 Zbl 0203.49901 |
Comments
References
| [a1] | H.L. Royden, "Real analysis" , Macmillan (1968) MR1013117 MR1532990 MR0151555 Zbl 1191.26002 Zbl 0704.26006 Zbl 0197.03501 Zbl 0121.05501 |
| [a2] | A.C. Zaanen, "Integration" , North-Holland (1967) MR0222234 Zbl 0175.05002 |
| [a3] | W. Rudin, "Principles of mathematical analysis" , McGraw-Hill (1953) MR0055409 Zbl 0052.05301 |
| [a4] | W. Rudin, "Real and complex analysis" , McGraw-Hill (1966) pp. 98 MR0210528 Zbl 0142.01701 |
| [a5] | A.E. Taylor, "General theory of functions and integration" , Blaisdell (1965) MR0178100 Zbl 0135.11301 |
| [a6] | C.D. Aliprantz, O. Burleinshaw, "Principles of real analysis" , North-Holland (1981) |
Borel measure. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Borel_measure&oldid=23583