Difference between revisions of "Bernoulli theorem"
(better MSC template) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 26: | Line 26: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> J. Bernoulli, "Ars conjectandi" , ''Werke'' , '''3''' , Birkhäuser (1975) pp. 107–286 (Original: Basle, 1713) {{MR|2349550}} {{MR|2393219}} {{MR|0935946}} {{MR|0850992}} {{MR|0827905}} {{ZBL|0957.01032}} {{ZBL|0694.01020}} {{ZBL|30.0210.01}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> A.A. Markov, "Wahrscheinlichkeitsrechung" , Teubner (1912) (Translated from Russian) {{MR|}} {{ZBL|39.0292.02}} </TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> S.N. Bernshtein, "Probability theory" , Moscow-Leningrad (1946) (In Russian) {{MR|1868030}} {{ZBL|}} </TD></TR></table> |
| Line 34: | Line 34: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> W. Feller, "An introduction to probability theory and its applications" , '''1''' , Wiley (1965) {{MR|0779091}} {{MR|0779090}} {{MR|0270403}} {{MR|0228020}} {{MR|1534302}} {{MR|0243559}} {{MR|0242202}} {{MR|0210154}} {{MR|1570945}} {{MR|0088081}} {{MR|1528130}} {{MR|0067380}} {{MR|0038583}} {{ZBL|0598.60003}} {{ZBL|0598.60002}} {{ZBL|0219.60003}} {{ZBL|0155.23101}} {{ZBL|0158.34902}} {{ZBL|0151.22403}} {{ZBL|0138.10207}} {{ZBL|0115.35308}} {{ZBL|0077.12201}} {{ZBL|0039.13201}} </TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> R.J. Serfling, "Approximation theorems of mathematical statistics" , Wiley (1980) pp. 6, 96 {{MR|0595165}} {{ZBL|0538.62002}} </TD></TR></table> |
Revision as of 10:29, 27 March 2012
2020 Mathematics Subject Classification: Primary: 60F05 [MSN][ZBL]
The (historically) original form of the (weak) law of large numbers. The theorem appeared in the fourth part of Jacob Bernoulli's book Ars conjectandi (The art of conjecturing). This part may be considered as the first serious study ever of probability theory. The book was published in 1713 by N. Bernoulli (a nephew of Jacob Bernoulli). The theorem deals with sequences of independent trials, in each one of which the probability of occurrence of some event ( "success" ) is 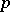 . Let
. Let  be the number of trials and let
be the number of trials and let 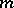 be the random variable equal to the number of successful events. The Bernoulli theorem states that, whatever the value of the positive numbers
be the random variable equal to the number of successful events. The Bernoulli theorem states that, whatever the value of the positive numbers  and
and 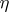 , the probability
, the probability 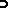 of the inequality
of the inequality
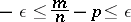 |
will be higher than 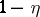 for all sufficiently large
for all sufficiently large  (
(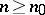 ). The proof of this theorem, which was given by Bernoulli and which was exclusively based on a study of the decrease of probabilities in the binomial distribution as one moves away from the most probable value, was accompanied by an inequality which made it possible to point out a certain bound for the given
). The proof of this theorem, which was given by Bernoulli and which was exclusively based on a study of the decrease of probabilities in the binomial distribution as one moves away from the most probable value, was accompanied by an inequality which made it possible to point out a certain bound for the given  if
if  and
and 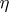 were given. Thus, it was found by Bernoulli that if
were given. Thus, it was found by Bernoulli that if 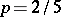 , the probability of the inequality
, the probability of the inequality
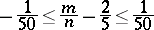 |
will be higher than 0.999 if 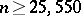 . By introducing a slight improvement in the original reasoning of Bernoulli, it is possible to conclude that it is sufficient to select a value of
. By introducing a slight improvement in the original reasoning of Bernoulli, it is possible to conclude that it is sufficient to select a value of  obeying the condition
obeying the condition
 |
which gives in turn, for the probability 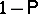 of the inequality
of the inequality
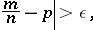 |
an estimate of the form
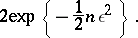 |
The condition obtained for the above example is 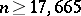 (more sophisticated estimates show that it is sufficient to take
(more sophisticated estimates show that it is sufficient to take 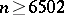 ; one may note, for the sake of comparison, that the de Moivre–Laplace theorem yields 6498 as the approximate value of
; one may note, for the sake of comparison, that the de Moivre–Laplace theorem yields 6498 as the approximate value of 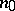 ). Other estimates for
). Other estimates for 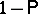 may be obtained using the Bernstein inequality and its analogues. See also Binomial distribution.
may be obtained using the Bernstein inequality and its analogues. See also Binomial distribution.
References
| [1] | J. Bernoulli, "Ars conjectandi" , Werke , 3 , Birkhäuser (1975) pp. 107–286 (Original: Basle, 1713) MR2349550 MR2393219 MR0935946 MR0850992 MR0827905 Zbl 0957.01032 Zbl 0694.01020 Zbl 30.0210.01 |
| [2] | A.A. Markov, "Wahrscheinlichkeitsrechung" , Teubner (1912) (Translated from Russian) Zbl 39.0292.02 |
| [3] | S.N. Bernshtein, "Probability theory" , Moscow-Leningrad (1946) (In Russian) MR1868030 |
Comments
References
| [a1] | W. Feller, "An introduction to probability theory and its applications" , 1 , Wiley (1965) MR0779091 MR0779090 MR0270403 MR0228020 MR1534302 MR0243559 MR0242202 MR0210154 MR1570945 MR0088081 MR1528130 MR0067380 MR0038583 Zbl 0598.60003 Zbl 0598.60002 Zbl 0219.60003 Zbl 0155.23101 Zbl 0158.34902 Zbl 0151.22403 Zbl 0138.10207 Zbl 0115.35308 Zbl 0077.12201 Zbl 0039.13201 |
| [a2] | R.J. Serfling, "Approximation theorems of mathematical statistics" , Wiley (1980) pp. 6, 96 MR0595165 Zbl 0538.62002 |
Bernoulli theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Bernoulli_theorem&oldid=23579