Difference between revisions of "Asymptotic negligibility"
From Encyclopedia of Mathematics
(better MSC template) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 11: | Line 11: | ||
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a013/a013720/a0137209.png" /></td> <td valign="top" style="width:5%;text-align:right;">(1)</td></tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a013/a013720/a0137209.png" /></td> <td valign="top" style="width:5%;text-align:right;">(1)</td></tr></table> | ||
| − | is satisfied, the individual terms <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a013/a013720/a01372010.png" /> are called asymptotically negligible (the variables <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a013/a013720/a01372011.png" /> then form a so-called zero triangular array). If condition (1) is met, one obtains the following important result: The class of limit distributions for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a013/a013720/a01372012.png" /> (<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a013/a013720/a01372013.png" /> are certain | + | is satisfied, the individual terms <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a013/a013720/a01372010.png" /> are called asymptotically negligible (the variables <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a013/a013720/a01372011.png" /> then form a so-called zero triangular array). If condition (1) is met, one obtains the following important result: The class of limit distributions for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a013/a013720/a01372012.png" /> (<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a013/a013720/a01372013.png" /> are certain "centering" constants) coincides with the class of infinitely-divisible distributions (cf. [[Infinitely-divisible distribution|Infinitely-divisible distribution]]). If the distributions of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a013/a013720/a01372014.png" /> converge to a limit distribution, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a013/a013720/a01372015.png" />, and the terms are identically distributed, condition (1) is automatically met. If the requirement for asymptotic negligibility is strengthened by assuming that for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a013/a013720/a01372016.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a013/a013720/a01372017.png" /> for all sufficiently large <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a013/a013720/a01372018.png" /> one has |
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a013/a013720/a01372019.png" /></td> <td valign="top" style="width:5%;text-align:right;">(2)</td></tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a013/a013720/a01372019.png" /></td> <td valign="top" style="width:5%;text-align:right;">(2)</td></tr></table> | ||
| Line 23: | Line 23: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> W. Feller, "An introduction to probability theory and its applications" , '''2''' , Wiley (1966) pp. 210 {{MR|0210154}} {{ZBL|0138.10207}} </TD></TR></table> |
Revision as of 10:29, 27 March 2012
2020 Mathematics Subject Classification: Primary: 60F99 [MSN][ZBL]
A property of random variables indicating that their individual contribution as components of a sum is small. This concept is important, for example, in the so-called triangular array. Let the random variables 
(
; 
) be mutually independent for each 
, and let
 |
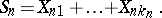If for all 
and 
, at sufficiently large values of 
, the inequality
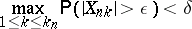 | (1) |
is satisfied, the individual terms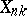 
are called asymptotically negligible (the variables 
then form a so-called zero triangular array). If condition (1) is met, one obtains the following important result: The class of limit distributions for 
(
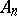are certain "centering" constants) coincides with the class of infinitely-divisible distributions (cf. Infinitely-divisible distribution). If the distributions of 
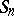converge to a limit distribution, 
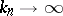, and the terms are identically distributed, condition (1) is automatically met. If the requirement for asymptotic negligibility is strengthened by assuming that for all 
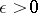and 
for all sufficiently large 
one has
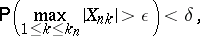 | (2) |
then the following statement is valid: If (2) is met, the limit distribution for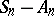 
can only be a normal distribution (in particular with variance equal to zero, i.e. a degenerate distribution).
Comments
References
| [a1] | W. Feller, "An introduction to probability theory and its applications" , 2 , Wiley (1966) pp. 210 MR0210154 Zbl 0138.10207 |
How to Cite This Entry:
Asymptotic negligibility. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Asymptotic_negligibility&oldid=23576
Asymptotic negligibility. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Asymptotic_negligibility&oldid=23576
This article was adapted from an original article by A.V. Prokhorov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article