Painlevé theorem

Painlevé's theorem on the solutions to analytic differential equations. The solutions to the differential equation 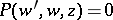cannot have movable (i.e. dependent on an arbitrary constant) essentially-singular points (cf. Movable singular point) and transcendental branch points, where 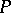is a polynomial in the unknown function 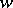and its derivative 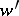, while 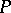is an analytic function in the independent variable .

Painlevé's theorem on analytic continuation. If 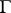is a rectifiable Jordan curve lying in a domain 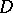in the complex -plane and if a function is continuous in and analytic in 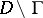, then 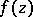is an analytic function in the entire domain 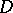[1], [2].

References

[1]	P. Painlevé, "Sur les lignes singulières des fonctions analytiques" , Paris (1887)
[2]	P. Painlevé, "Leçons sur la théorie analytique des équations différentielles, professées à Stockholm (1895)" , Paris (1897)
[3]	V.V. Golubev, "Vorlesungen über Differentialgleichungen im Komplexen" , Deutsch. Verlag Wissenschaft. (1958) (Translated from Russian)

Comments

For Painlevé's theorem on differential equations see also [a1], [a4].

If in 2) 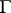is not required to be rectifiable, the analytic continuation need not be possible, cf. [a1], [a2].

References

[a1]	J.B. Garnett, "Analytic capacity and measure" , Lect. notes in math. , 297 , Springer (1972)
[a2]	J. Wermer, "Banach algebras and several complex variables" , Springer (1976) pp. Chapt. 13
[a3]	E.L. Ince, "Ordinary differential equations" , Dover, reprint (1956) pp. §§3.6, 3.51, 4.7, A.5
[a4]	E. Hille, "Lectures on ordinary differential equations" , Addison-Wesley (1969)