Difference between revisions of "Fréchet differential"
Ulf Rehmann (talk | contribs) m (moved Fréchet differential to Frechet differential: ascii title) |
Ulf Rehmann (talk | contribs) m (moved Frechet differential to Fréchet differential over redirect: accented title) |
(No difference)
| |
Revision as of 07:54, 26 March 2012
at a point 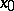 of a mapping
of a mapping 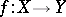 of a normed space
of a normed space 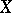 into a normed space
into a normed space 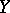
The mapping 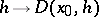 which is linear and continuous from
which is linear and continuous from 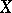 into
into 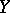 and has the property that
and has the property that
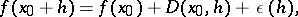 | (1) |
where
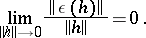 |
If a mapping 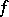 admits an expansion (1) at a point
admits an expansion (1) at a point 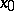 , then it is said to be Fréchet differentiable, and the actual operator
, then it is said to be Fréchet differentiable, and the actual operator
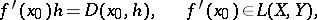 |
is called the Fréchet derivative.
For a function 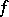 in a finite number of variables, the Fréchet differential is the linear function
in a finite number of variables, the Fréchet differential is the linear function
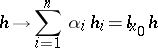 |
that has the property that
 | (2) |
where 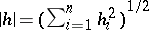 or any other equivalent norm in
or any other equivalent norm in  . Here
. Here 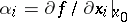 are the partial derivatives of
are the partial derivatives of 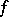 at
at 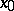 .
.
Definition (2), which is now commonplace, apparently first appeared in an explicit form in the lectures of K. Weierstrass (1861, see [1]). At the end of the 19th century this definition gradually came into the textbooks (see [2], [3] and others). But at the time when M. Fréchet began to develop infinite-dimensional analysis, the now classical definition of the differential was so far from commonplace that even Fréchet himself supposed that his definition of the differential in an infinite-dimensional space was a new concept in the finite-dimensional case too. Nowadays the term is only used in relation to infinite-dimensional mappings. See Gâteaux differential; Differential.
References
| [1] | P. Dugac, "Eléments d'analyse de Karl Weierstrass" , Paris (1972) |
| [2] | O. Stolz, "Grundzüge der Differential- und Integralrechnung" , 1 , Teubner (1893) |
| [3] | W. Young, "The fundamental theorems of the differential calculus" , Cambridge Univ. Press (1910) |
| [4] | M. Fréchet, "Sur la notion de différentielle" C.R. Acad. Sci. Paris , 152 (1911) pp. 845–847; 1050–1051 |
| [5] | M. Fréchet, "Sur la notion de différentielle totale" Nouvelles Ann. Math. Sér. 4 , 12 (1912) pp. 385–403; 433–449 |
| [6] | A.N. Kolmogorov, S.V. Fomin, "Elements of the theory of functions and functional analysis" , 1–2 , Graylock (1957–1961) (Translated from Russian) |
| [7] | V.M. Alekseev, V.M. Tikhomirov, S.V. Fomin, "Optimal control" , Consultants Bureau (1987) (Translated from Russian) |
Fréchet differential. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Fr%C3%A9chet_differential&oldid=23282