Difference between revisions of "Rao-Blackwell-Kolmogorov theorem"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (moved Rao–Blackwell–Kolmogorov theorem to Rao-Blackwell-Kolmogorov theorem: ascii title) |
(No difference)
| |
Revision as of 18:54, 24 March 2012
A proposition from the theory of statistical estimation on which a method for the improvement of unbiased statistical estimators is based.
Let 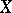 be a random variable with values in a sample space
be a random variable with values in a sample space 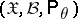 ,
, 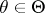 , such that the family of probability distributions
, such that the family of probability distributions 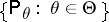 has a sufficient statistic
has a sufficient statistic 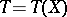 , and let
, and let 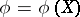 be a vector statistic with finite matrix of second moments. Then the mean
be a vector statistic with finite matrix of second moments. Then the mean 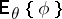 of
of 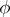 exists and, moreover, the conditional mean
exists and, moreover, the conditional mean 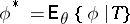 is an unbiased estimator for
is an unbiased estimator for 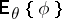 , that is,
, that is,
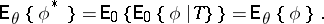 |
The Rao–Blackwell–Kolmogorov theorem states that under these conditions the quadratic risk of 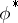 does not exceed the quadratic risk of
does not exceed the quadratic risk of 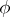 , uniformly in
, uniformly in 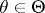 , i.e. for any vector
, i.e. for any vector  of the same dimension as
of the same dimension as 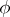 , the inequality
, the inequality
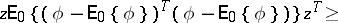 |
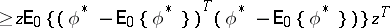 |
holds for any 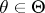 . In particular, if
. In particular, if 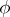 is a one-dimensional statistic, then for any
is a one-dimensional statistic, then for any 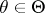 the variance
the variance 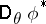 of
of  does not exceed the variance
does not exceed the variance 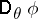 of
of 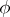 .
.
In the most general situation the Rao–Blackwell–Kolmogorov theorem states that averaging over a sufficient statistic does not lead to an increase of the risk with respect to any convex loss function. This implies that good statistical estimators should be looked for only in terms of sufficient statistics, that is, in the class of functions of sufficient statistics.
In case the family 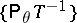 is complete, that is, when the function of
is complete, that is, when the function of 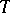 that is almost-everywhere equal to zero is the only unbiased estimator based on
that is almost-everywhere equal to zero is the only unbiased estimator based on 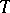 for zero, the unbiased estimator with uniformly minimal risk provided by the Rao–Blackwell–Kolmogorov theorem is unique. Thus, the Rao–Blackwell–Kolmogorov theorem gives a recipe for constructing best unbiased estimators: one has to take some unbiased estimator and then average it over a sufficient statistic. That is how the best unbiased estimator for the distribution function of the normal law is constructed in the following example, which is due to A.N. Kolmogorov.
for zero, the unbiased estimator with uniformly minimal risk provided by the Rao–Blackwell–Kolmogorov theorem is unique. Thus, the Rao–Blackwell–Kolmogorov theorem gives a recipe for constructing best unbiased estimators: one has to take some unbiased estimator and then average it over a sufficient statistic. That is how the best unbiased estimator for the distribution function of the normal law is constructed in the following example, which is due to A.N. Kolmogorov.
Example. Given a realization of a random vector 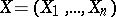 whose components
whose components 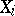 ,
, 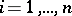 ,
, 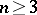 , are independent random variables subject to the same normal law
, are independent random variables subject to the same normal law 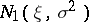 , it is required to estimate the distribution function
, it is required to estimate the distribution function
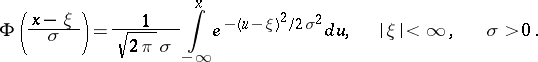 |
The parameters 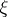 and
and 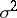 are supposed to be unknown. Since the family
are supposed to be unknown. Since the family
 |
of normal laws has a complete sufficient statistic 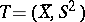 , where
, where
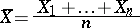 |
and
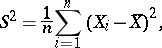 |
the Rao–Blackwell–Kolmogorov theorem can be used for the construction of the best unbiased estimator for the distribution function 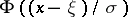 . As an initial statistic
. As an initial statistic 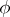 one may use, e.g., the empirical distribution function constructed from an arbitrary component
one may use, e.g., the empirical distribution function constructed from an arbitrary component 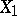 of
of 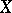 :
:
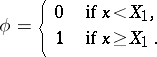 |
This is a trivial unbiased estimator for 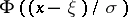 , since
, since
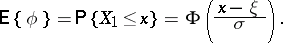 |
Averaging of 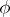 over the sufficient statistic
over the sufficient statistic 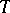 gives the estimator
gives the estimator
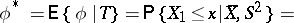 | (1) |
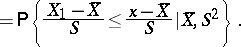 |
Since the statistic
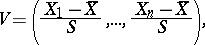 |
which is complementary to 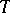 , has a uniform distribution on the
, has a uniform distribution on the 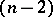 -dimensional sphere of radius
-dimensional sphere of radius  and, therefore, depends neither on the unknown parameters
and, therefore, depends neither on the unknown parameters 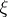 and
and 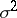 nor on
nor on 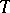 , the same is true for
, the same is true for 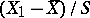 and
and
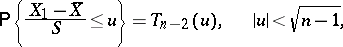 | (2) |
where
 | (3) |
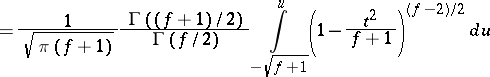 |
is the Thompson distribution with 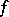 degrees of freedom. Thus, (1)–(3) imply that the best unbiased estimator for
degrees of freedom. Thus, (1)–(3) imply that the best unbiased estimator for 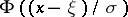 obtained from
obtained from  independent observations
independent observations 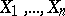 is
is
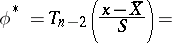 |
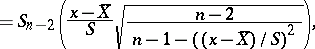 |
where 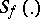 is the Student distribution with
is the Student distribution with 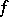 degrees of freedom.
degrees of freedom.
References
| [1] | A.N. Kolmogorov, "Unbiased estimates" Izv. Akad. Nauk SSSR Ser. Mat. , 14 : 4 (1950) pp. 303–326 (In Russian) |
| [2] | C.R. Rao, "Linear statistical inference and its applications" , Wiley (1965) |
| [3] | B.L. van der Waerden, "Mathematische Statistik" , Springer (1957) |
| [4] | D. Blackwell, "Conditional expectation and unbiased sequential estimation" Ann. Math. Stat. , 18 (1947) pp. 105–110 |
Comments
In the Western literature this theorem is mostly referred to as the Rao–Blackwell theorem.
Rao-Blackwell-Kolmogorov theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Rao-Blackwell-Kolmogorov_theorem&oldid=22963