Montesinos-Nakanishi conjecture

Any link can be reduced to a trivial link by a sequence of -moves (that is, moves which add three half-twists into two parallel arcs of a link).

The conjecture has been proved for links up to 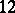crossings, 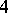-bridge links and five-braid links except one family represented by the square of the centre of the -braid group. This link, which can be reduced by -moves to a -crossings link, is the smallest known link for which the conjecture is open (as of 2001).

The conjecture has its stronger version that any -tangle can be reduced by -moves to one of -tangles (with possible additional trivial components), where .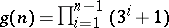

References

[a1]	R. Kirby, "Problems in low-dimensional topology" W. Kazez (ed.) , Geometric Topology (Proc. Georgia Internat. Topol. Conf. 1993) , Stud. Adv. Math. , 2:2 , Amer. Math. Soc. /IP (1997) pp. 35–473
[a2]	Q. Chen, "The -move conjecture for -braids" , Knots in Hellas '98 (Proc. Internat. Conf. Knot Theory and Its Ramifications , Knots and Everything , 24 (2000) pp. 36–47
[a3]	J.H. Przytycki, T. Tsukamoto, "The fourth skein module and the Montesinos–Nakanishi conjecture for -algebraic links" J. Knot Th. Ramifications , to appear (2001)
[a4]	H.R. Morton, "Problems" J.S. Birman (ed.) A. Libgober (ed.) , Braids (Santa Cruz, 1986) , Contemp. Math. , 78 , Amer. Math. Soc. (1988) pp. 557–574