Difference between revisions of "Lieb-Thirring inequalities"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (moved Lieb–Thirring inequalities to Lieb-Thirring inequalities: ascii title) |
(No difference)
| |
Revision as of 18:53, 24 March 2012
Inequalities concerning the negative
eigenvalues of the
Schrödinger operator
(cf. also
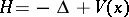 |
on
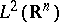 ,
,
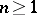 .
.
With
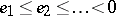
denoting the negative eigenvalue(s) of
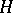
(if any), the Lieb–Thirring
inequalities state that for suitable
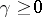
and constants
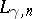 ,
,
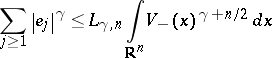 | (a1) |
with
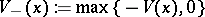 .
.
When
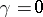 ,
,
the left-hand side is just the number of negative eigenvalues. Such an
inequality
(a1)
can hold if and only if
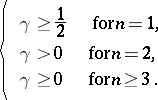 | (a2) |
The cases
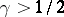 ,
,
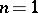 ,
,
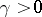 ,
,
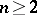 ,
,
were established by
E.H. Lieb
and
W.E. Thirring
in connection with their proof of
stability of matter.
The case
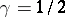 ,
,
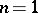 ,
,
was established by
T. Weidl
The case
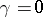 ,
,
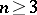 ,
,
was established independently by
M. Cwikel
Lieb
and
G.V. Rosenbljum
by different methods and is known as the
CLR bound;
the smallest known
value (as of
1998)
for
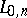
is in
[a6],
[a7].
Closely associated with the inequality
(a1)
is the
semi-classical approximation
for
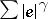 ,
,
which serves as a heuristic motivation for
(a1).
It is
(cf.
[a14]):
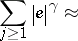 |
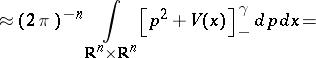 |
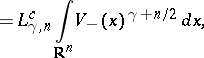 |
with
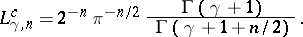 |
Indeed,
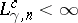
for all
 ,
,
whereas
(a1)
holds only for the range given in
(a2).
It is easy to prove (by considering
with
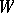
smooth and
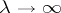 )
)
that
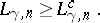 |
An interesting, and mostly open
(1998)
problem is to determine the sharp
value
of the constant
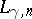 ,
,
especially to find those cases in which
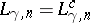 .
.
M. Aizenman
and
Lieb
proved that the ratio
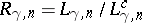
is a monotonically non-increasing function of
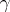 .
.
Thus, if
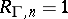
for some
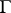 ,
,
then
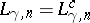
for all
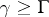 .
.
The equality
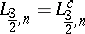
was proved for
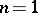
in
and for
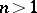
in
by
A. Laptev
and
Weidl.
(See also
[a1].)
The following sharp constants are known:
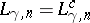 ,
,
all
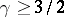 ,
,
[a3],
[a2];
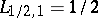 ,
,
There is strong support for the
conjecture
that
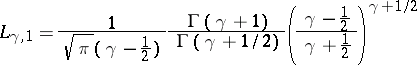 | (a3) |
for
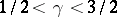 .
.
Instead of considering all the negative eigenvalues as in
(a1),
one can consider just
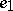 .
.
Then for
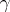
as in
(a2),
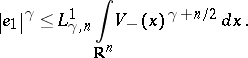 |
Clearly,
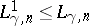 ,
,
but equality can hold, as in the cases
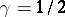
and
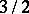
for
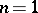 .
.
Indeed, the conjecture in
(a3)
amounts to
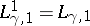
for
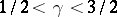 .
.
The sharp value
(a3)
of
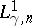
is obtained by solving a differential equation
It has been conjectured that for
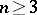 ,
,
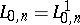 .
.
In any case,
B. Helffer
and
D. Robert
showed that for all

and all
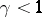 ,
,
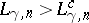 .
.
The sharp constant
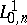 ,
,
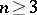 ,
,
is related to the sharp constant
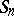
in the
Sobolev inequality
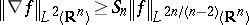 | (a4) |
by
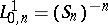 .
.
By a
"duality argument"
the case
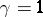
in
(a1)
can be converted into the following bound for the
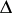 .
.
This bound is
referred to as a
Lieb–Thirring kinetic energy inequality
and its most important application is to the
stability of matter
[a8],
Let
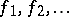
be
any
orthonormal sequence (finite or infinite, cf. also
in
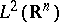
such that
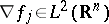
for all
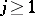 .
.
Associated with this sequence is a
"density"
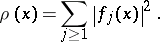 | (a5) |
Then, with
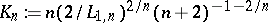 ,
,
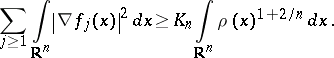 | (a6) |
This can be extended to
anti-symmetric functions
in
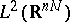 .
.
If
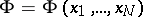
is such a function, one defines, for
 ,
,
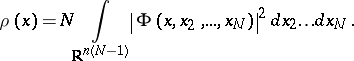 |
Then, if
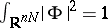 ,
,
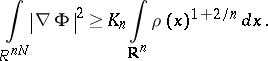 | (a7) |
Note that the choice
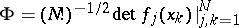
with
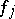
orthonormal reduces the general case
(a7)
to
(a6).
If the conjecture
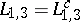
is correct, then the bound in
(a7)
equals the
Thomas–Fermi kinetic energy Ansatz
(cf.
and hence it is a challenge to prove this conjecture. In the meantime,
see
[a7],
for the best available constants to date
(1998).
Of course,
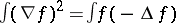 .
.
Inequalities of the type
(a7)
can be found for other powers of
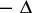
than the first power. The first example of this kind, due to
I. Daubechies
and one of the most important physically, is to replace
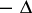
by
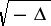
in
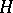 .
.
Then an inequality similar to
(a1)
holds with
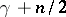
replaced by
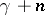
(and with a different
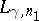 ,
,
of course). Likewise there is an analogue of
(a7)
with
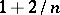
replaced by
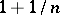 .
.
All proofs of
(a1)
(except
and
actually
proceed by finding an upper bound to
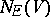 ,
,
the number of eigenvalues of
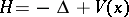
that are below
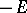 .
.
Then, for
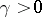 ,
,
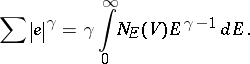 |
Assuming
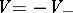
(since
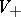
only raises the eigenvalues),
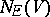
is most accessible via the positive semi-definite
Birman–Schwinger kernel
(cf.
[a4])
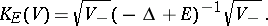 |
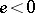
is an eigenvalue of
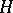
if and only if
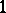
is an eigenvalue of
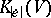 .
.
Furthermore,
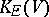
is
operator
that is monotone decreasing in
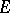 ,
,
and hence
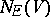
equals the number of eigenvalues of
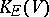
that are greater than
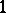 .
.
An important generalization of
(a1)
is to replace
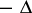
in
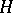
by
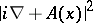 ,
,
where
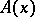
is some arbitrary vector field in
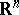
(called a
magnetic vector potential).
Then
(a1)
still holds, but it is not known if the sharp value of

changes. What is known is that all
presently
(1998)
known values of
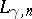
are unchanged. It is also known that
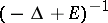 ,
,
as a kernel in
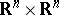 ,
,
is pointwise greater than the absolute value of the kernel
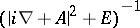 .
.
There is another family of inequalities for orthonormal functions,
which is closely related to
(a1)
and to the CLR
bound
[a9].
As before, let
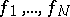
be
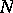
orthonormal functions in
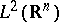
and set
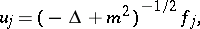 |
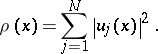 |
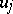
is a
(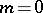 )
)
or a
(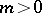 )
)
of
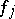 .
.
If
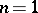
and
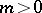 ,
,
then
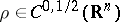
and
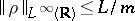 .
.
If
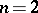
and
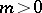 ,
,
then for all
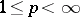 ,
,
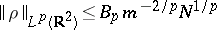 .
.
If
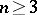 ,
,
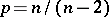
and
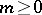
(including
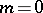 ),
),
then
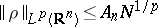 .
.
Here,
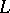 ,
,
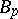 ,
,
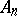
are universal constants. Without the orthogonality,
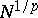
would have to be replaced by
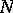 .
.
Further generalizations are
possible
[a9].
References
| [a1] |
R. Benguria, M. Loss, "A simple proof of a theorem of Laptev and Weidl" Preprint (1999) |
| [a2] |
A. Laptev, T. Weidl, "Sharp Lieb–Thirring inequalities in high dimensions" Acta Math. (in press 1999) |
| [a3] |
M.A. Aizenman, E.H. Lieb, "On semiclassical bounds for eigenvalues of Schrödinger operators" Phys. Lett. , 66A (1978) pp. 427–429 |
| [a4] |
B. Simon, "Functional integration and quantum physics" , Pure Appl. Math. , 86 , Acad. Press (1979) |
| [a5] |
Ph. Blanchard, J. Stubbe, "Bound states for Schrödinger Hamiltonians: phase space methods and applications" Rev. Math. Phys. , 8 (1996) pp. 503–547 |
| [a6] |
E.H. Lieb, "The numbers of bound states of one-body Schrödinger operators and the Weyl problem" , Geometry of the Laplace Operator (Honolulu, 1979) , Proc. Symp. Pure Math. , 36 , Amer. Math. Soc. (1980) pp. 241–251 |
| [a7] |
E.H. Lieb, "On characteristic exponents in turbulence" Comm. Math. Phys. , 92 (1984) pp. 473–480 |
| [a8] |
E.H. Lieb, "Kinetic energy bounds and their applications to the stability of matter" H. Holden (ed.) A. Jensen (ed.) , Schrödinger Operators (Proc. Nordic Summer School, 1988) , Lecture Notes Physics , 345 , Springer (1989) pp. 371–382 |
| [a9] |
E.H. Lieb, "An
J. Funct. Anal. , 51 (1983) pp. 159–165 |
| [a10] |
G.V. Rosenbljum, "Distribution of the discrete spectrum of singular differential operators" Dokl. Akad. Nauk SSSR , 202 (1972) pp. 1012–1015 ((The details are given in: Izv. Vyss. Uchebn. Zaved. Mat. 164 (1976), 75-86 (English transl.: Soviet Math. (Izv. VUZ) 20 (1976), 63-71))) |
| [a11] |
D. Hundertmark, E.H. Lieb, L.E. Thomas, "A sharp bound for an eigenvalue moment of the one-dimensional Schrödinger operator" Adv. Theor. Math. Phys. , 2 (1998) pp. 719–731 |
| [a12] |
B. Helffer, D. Robert, "Riesz means of bound states and semi-classical limit connected with a Lieb–Thirring conjecture, II" Ann. Inst. H. Poincaré Phys. Th. , 53 (1990) pp. 139–147 |
| [a13] |
I. Daubechies, "An uncertainty principle for fermions with generalized kinetic energy" Comm. Math. Phys. , 90 (1983) pp. 511–520 |
| [a14] |
E.H. Lieb, W. Thirring, "Inequalities for the moments of the eigenvalues of the Schrödinger Hamiltonian and their relation to Sobolev inequalities" E. Lieb (ed.) B. Simon (ed.) A. Wightman (ed.) , Studies in Mathematical Physics: Essays in Honor of Valentine Bargmann , Princeton Univ. Press (1976) pp. 269–303 ((See also: W. Thirring (ed.), The stability of matter: from the atoms to stars, Selecta of E.H. Lieb, Springer, 1977)) |
| [a15] |
M. Cwikel, "Weak type estimates for singular values and the number of bound states of Schrödinger operators" Ann. Math. , 106 (1977) pp. 93–100 |
| [a16] |
T. Weidl, "On the Lieb–Thirring constants
Comm. Math. Phys. , 178
(1996) pp. 135–146 |
Elliott H. Lieb
Copyright to this article is held by Elliott Lieb.
Lieb-Thirring inequalities. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Lieb-Thirring_inequalities&oldid=22739
 bound for the Riesz and Bessel potentials of orthonormal functions"
bound for the Riesz and Bessel potentials of orthonormal functions"
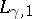 for
for
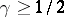 "
"