Federer-Fleming deformation theorem

The Federer–Fleming deformation theorem can be considered as one of the central results in the theory of integral currents, created by H. Federer and W.H. Fleming at the end of 1950s, [a1]. The notion of an integral current was introduced to meet all the requirements of the concept of "k-dimensional domain of integration in Euclidean n-space" and combines the smoothness properties of differentiable manifolds and the combinatorial structure of polyhedral chains with integer coefficients. The notion of integral current provides a powerful instrument for solving geometrical variational problems like the Plateau problem.

The deformation theorem shows how one can deform normal and integral currents into similar currents with supports in the appropriate skeletons of a standard cubical cell complex with given cube edge, and gives estimates for the masses of the currents.

Let 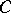denote the standard cubical complex in the Euclidean space 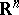generated by the cubes with edge and with centres at the integer points. Let 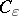denote the complex obtained from 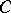by -homothety (cf. Homothety). As always, let 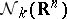denote the space of normal currents in 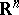, and let 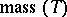be the mass of the current 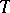(cf. also Differential form; Mass and co-mass).

The Federer–Fleming deformation theorem reads: Let 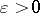be an arbitrary positive number. Then any -dimensional normal current in 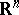can be represented as a sum

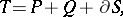where

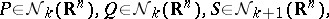with the following properties:

1) The current is a polyhedral chain of 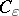with real coefficients. If is an integral current, then the coefficients of 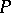are integers.

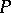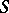2) The supports of and lie in the -neighbourhood of the support of 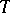, and the supports of 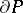and lie in the -neighbourhood of .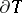

3) For the masses of 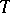, , 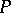, 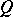and 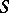the following estimates hold:

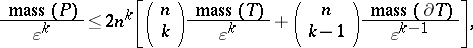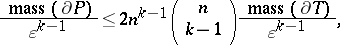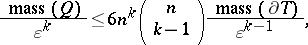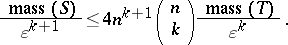4) If 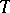is an integral current, then so are 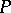, and .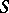

5) If 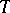is an (integral) Lipschitz chain, so are 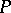, 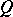and .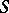

6) If is an (integral) Lipschitz chain, so is .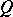

As a consequence, one can obtain the following result: For each integral current there exists a sequence of integral Lipschitz chains 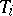such that

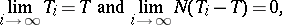where .

As other applications of the theorem, one can obtain the theorem about isomorphism between the integer singular homology groups of and the homology groups of the integral current chain complex 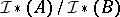, where 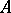and 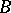are local Lipschitz neighbourhood retracts in 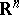; the isoperimetric inequalities for integral currents; etc. Some modern applications of the theorem can be found in [a2], [a3].

References

[a1]	H. Federer, W.H. Fleming, "Normal and integral currents" Ann. of Math. , 72 : 3 (1960) pp. 458–520
[a2]	Dao Trong Thi, A.T. Fomenko, "Minimal surfaces, stratified multivarifolds and the Plateau problem" , Amer. Math. Soc. (1991)
[a3]	A.T. Fomenko, "Variational principles in topology: multidimensional minimal surface theory" , Kluwer Acad. Publ. (1990)