Difference between revisions of "Bellman-Harris process"
(better MSC template) |
Ulf Rehmann (talk | contribs) m (moved Bellman–Harris process to Bellman-Harris process: ascii title) |
(No difference)
| |
Revision as of 18:50, 24 March 2012
2020 Mathematics Subject Classification: Primary: 60J80 [MSN][ZBL]
A special case of an age-dependent branching process (cf. Branching process, age-dependent). It was first studied by R. Bellman and T.E. Harris [1]. In the Bellman–Harris process it is assumed that particles live, independently of each other, for random periods of time, and produce a random number of new particles at the end of their life time. If 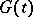 is the distribution function of the life times of the individual particles, if
is the distribution function of the life times of the individual particles, if 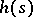 is the generating function of the number of direct descendants of one particle, and if at time
is the generating function of the number of direct descendants of one particle, and if at time 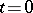 the age of the particle was zero, then the generating function
the age of the particle was zero, then the generating function 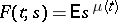 of the number of particles
of the number of particles 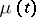 satisfies the non-linear integral equation
satisfies the non-linear integral equation
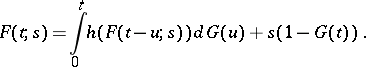 |
If
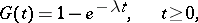 |
the Bellman–Harris process is a Markov branching process with continuous time.
References
| [1] | R. Bellman, T.E. Harris, "On the theory of age-dependent stochastic branching processes" Proc. Nat. Acad. Sci. USA , 34 (1948) pp. 601–604 |
Bellman-Harris process. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Bellman-Harris_process&oldid=22083