Difference between revisions of "General position"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 1: | Line 1: | ||
''generic position'' | ''generic position'' | ||
| − | A term used in such phrases as | + | A term used in such phrases as "the objects O in general (generic) position have the property S (or properties Si)" , "S is a property of general position" , "reduction (transformation) to general position" , the precise meaning of which depends on the context. Usually the set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043690/g0436901.png" /> of all objects considered has a structure allowing certain subsets <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043690/g0436902.png" /> to be regarded as "small" , "negligible" or, conversely, "large" , "massive" ; <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043690/g0436903.png" /> is then regarded as a "property of general position" if the objects possessing it form a "large" subset of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043690/g0436904.png" />. <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043690/g0436905.png" /> usually has one of the following structures: a) an [[Algebraic variety|algebraic variety]]; b) a [[Differentiable manifold|differentiable manifold]] (possibly infinite-dimensional); c) a topological space, most often a [[Baire space|Baire space]] in the first meaning of this term; or d) a [[Measure space|measure space]]. The following are considered "small" respectively: algebraic subvarieties (of lower dimension), differentiable submanifolds and finite or countable unions of them, nowhere-dense sets or sets of the first category, sets of measure zero. A set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043690/g0436906.png" /> is regarded as "large" if its complement is "small" . One then also says that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043690/g0436907.png" /> contains "most" or "almost all" of the objects of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043690/g0436908.png" />, and a property <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043690/g0436909.png" /> satisfied by almost all objects is called "typical" , or a property of general position. One frequently speaks of a "typical" object, or an object being of general position or an object in general position, implying (sometimes tacitly) that there are one or more "typical" properties (of what kind should be clear from the context) and that one is concerned with an object having these properties. |
| − | In a weaker sense, a | + | In a weaker sense, a "large" subset in cases c) and d) may mean a subset of the second category in a non-empty open subset of the space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043690/g04369010.png" /> or a subset of positive measure. Then one says that this set of objects "cannot be neglected" (but one no longer says that it is "typical" ). |
| − | In cases a) and b) a | + | In cases a) and b) a "small" set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043690/g04369011.png" /> has positive codimension <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043690/g04369012.png" />. It is natural to say that as <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043690/g04369013.png" /> gets larger, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043690/g04369014.png" /> gets smaller. A situation close to b) (but more general) is when one can speak of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043690/g04369015.png" />-parameter families of objects <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043690/g04369016.png" />, depending sufficiently smoothly on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043690/g04369017.png" /> (scalar) parameters, and when all possible such families form a Baire space. If almost all (in sense c)) of these families do not contain objects of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043690/g04369018.png" />, then one says that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043690/g04369019.png" />, and if this is true for any <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043690/g04369020.png" />, then one puts <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043690/g04369021.png" />. Considerations of codimension play an important part in [[Bifurcation|bifurcation]] theory and the theory of [[Singularities of differentiable mappings|singularities of differentiable mappings]] (see also [[#References|[8]]]). |
| − | Certain operations <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043690/g04369022.png" /> may act on the objects; the set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043690/g04369023.png" /> of these operations is usually a group, or at least a semi-group with an identity <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043690/g04369024.png" />. One speaks of | + | Certain operations <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043690/g04369022.png" /> may act on the objects; the set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043690/g04369023.png" /> of these operations is usually a group, or at least a semi-group with an identity <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043690/g04369024.png" />. One speaks of "reduction of an object O to general position by the operation g" when it is clear from the context what properties are being considered; "reduction" means that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043690/g04369025.png" /> has these properties. Like <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043690/g04369026.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043690/g04369027.png" /> is usually provided with a structure allowing one to speak of a "large" set of operations, or to say that the operation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043690/g04369028.png" /> taking <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043690/g04369029.png" /> to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043690/g04369030.png" />, with the necessary properties, can be chosen arbitrary close to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043690/g04369031.png" /> ( "reduction to general position by a small shift" ). |
| − | For example, a line and a circle in the plane in general position either do not intersect or intersect in two points. In this case the object is the pair <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043690/g04369032.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043690/g04369033.png" /> is the line and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043690/g04369034.png" /> the circle, and the operations may be taken as Euclidean motions (or just parallel translations), acting on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043690/g04369035.png" /> with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043690/g04369036.png" /> fixed. The set of all possible objects <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043690/g04369037.png" /> and the group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043690/g04369038.png" /> are naturally endowed with the structures mentioned above, and general position can be interpreted according to each of the versions. Originally, the term general position was used in similar geometrical problems, and thence it was transferred to areas of mathematics of a geometrical character, or at least considerably influenced by geometry (although arguments involving sets of the second category or of full measure are used outside these areas). To the present day, the term | + | For example, a line and a circle in the plane in general position either do not intersect or intersect in two points. In this case the object is the pair <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043690/g04369032.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043690/g04369033.png" /> is the line and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043690/g04369034.png" /> the circle, and the operations may be taken as Euclidean motions (or just parallel translations), acting on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043690/g04369035.png" /> with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043690/g04369036.png" /> fixed. The set of all possible objects <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043690/g04369037.png" /> and the group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043690/g04369038.png" /> are naturally endowed with the structures mentioned above, and general position can be interpreted according to each of the versions. Originally, the term general position was used in similar geometrical problems, and thence it was transferred to areas of mathematics of a geometrical character, or at least considerably influenced by geometry (although arguments involving sets of the second category or of full measure are used outside these areas). To the present day, the term "general position" is often applied to a situation immediately generalizing the above example, when one speaks of the [[Transversality|transversality]] of two submanifolds in some ambient manifold (or the related situation of transversality of the self-intersections of an immersed submanifold). In particular, in geometric topology (considering piecewise-linear or topological manifolds and the corresponding classes of mappings) the term "general position" is used almost exclusively as a synonym of transversality. |
In algebraic geometry simple examples (like the one above) can easily be analyzed by elimination theory, where the ground field may be completely arbitrary (usually algebraically closed). There are theorems on general position in more complicated situations (for example, [[Bertini theorems|Bertini theorems]], and the [[Lefschetz theorem|Lefschetz theorem]] on a hyperplane section); in studying the action of algebraic groups on algebraic varieties points in general position (cf. [[Point in general position|Point in general position]]) play a large part [[#References|[1]]]. | In algebraic geometry simple examples (like the one above) can easily be analyzed by elimination theory, where the ground field may be completely arbitrary (usually algebraically closed). There are theorems on general position in more complicated situations (for example, [[Bertini theorems|Bertini theorems]], and the [[Lefschetz theorem|Lefschetz theorem]] on a hyperplane section); in studying the action of algebraic groups on algebraic varieties points in general position (cf. [[Point in general position|Point in general position]]) play a large part [[#References|[1]]]. | ||
| Line 15: | Line 15: | ||
In differential topology and the theory of singularities of differentiable mappings, general position is used very extensively. Proofs are usually carried out by means of Sard's theorem or its corollaries, and the Abraham and Thom transversality theorems (see [[#References|[2]]], [[#References|[3]]]), which are more suitable for immediate application. In the infinite-dimensional case Sard's theorem is not valid, but weaker results that are sometimes sufficient can be obtained (see [[#References|[4]]], [[#References|[5]]], [[#References|[14]]]). | In differential topology and the theory of singularities of differentiable mappings, general position is used very extensively. Proofs are usually carried out by means of Sard's theorem or its corollaries, and the Abraham and Thom transversality theorems (see [[#References|[2]]], [[#References|[3]]]), which are more suitable for immediate application. In the infinite-dimensional case Sard's theorem is not valid, but weaker results that are sometimes sufficient can be obtained (see [[#References|[4]]], [[#References|[5]]], [[#References|[14]]]). | ||
| − | There are several results on | + | There are several results on "typical" properties in the theory of smooth dynamical systems. Most of them are proved (particularly, in bifurcation theory) by reduction to Sard's theorem; positive results not connected with this reduction are few (see [[#References|[6]]], [[#References|[7]]], [[#References|[9]]], [[#References|[10]]], and the references to [[Rough system|Rough system]]). A characteristic of the theory of smooth dynamical systems is the presence of an essential distinction between general position in the topological and metric sense (c) and d) above) , [[#References|[15]]]. |
For general position in the differential geometry of manifolds see [[#References|[12]]], [[#References|[13]]]. | For general position in the differential geometry of manifolds see [[#References|[12]]], [[#References|[13]]]. | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> D. Mumford, "Geometric invariant theory" , Springer (1965) {{MR|0214602}} {{ZBL|0147.39304}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> S. Lang, "Introduction to differentiable manifolds" , Interscience (1967) pp. App. III {{MR|1931083}} {{MR|1532744}} {{MR|0155257}} {{ZBL|1008.57001}} {{ZBL|0103.15101}} </TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> V.I. Arnol'd, "Chapitres supplémentaires de la théorie des équations différentielles ordinaires" , MIR (1980) (Translated from Russian)</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> J. Eells, J. McAlpin, "An approximate Morse–Sard theorem" ''J. Math. Mech.'' , '''17''' : 11 (1968) pp. 1055–1064 {{MR|0226680}} {{ZBL|0159.24901}} </TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> F. Quinn, "Transversal approximation on Banach manifolds" S.-S. Chern (ed.) S. Smale (ed.) , ''Global analysis'' , ''Proc. Symp. Pure Math.'' , '''14''' , Amer. Math. Soc. (1970) pp. 213–222 {{MR|0264713}} {{ZBL|0206.25705}} </TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> C. Gutierrez, "Structural stability of flows on the torus with a cross-cap" ''Trans. Amer. Math. Soc.'' , '''241''' (1978) pp. 311–320 {{MR|}} {{ZBL|}} </TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> C. Gutierrez, "Smooth nonorientable nontrivial recurrence on two-manifolds" ''J. Differential Equations'' , '''29''' : 3 (1978) pp. 388–395 {{MR|0507486}} {{ZBL|0413.58018}} </TD></TR><TR><TD valign="top">[8]</TD> <TD valign="top"> H. Kurland, J. Robbin, "Infinite codimension and transversality" A. Manning (ed.) , ''Dynamical systems (Warwick, 1974)'' , ''Lect. notes in math.'' , '''468''' , Springer (1975) pp. 135–150 {{MR|0649273}} {{ZBL|0317.58011}} </TD></TR><TR><TD valign="top">[9]</TD> <TD valign="top"> F. Takens, "Tolerance stability" A. Manning (ed.) , ''Dynamical systems (Warwick, 1974)'' , ''Lect. notes in math.'' , '''468''' , Springer (1975) pp. 293–304 {{MR|0650298}} {{ZBL|0321.54022}} </TD></TR><TR><TD valign="top">[10]</TD> <TD valign="top"> V.A. Dobrynskii, A.N. Sharkovskii, "Typicalness of dynamical systems almost all paths of which are stable under permanently acting perturbations" ''Soviet Math. Dokl.'' , '''14''' : 4 (1973) pp. 997–1000 ''Dokl. Akad. Nauk SSSR'' , '''211''' : 2 (1973) pp. 273–276 {{MR|}} {{ZBL|}} </TD></TR><TR><TD valign="top">[11a]</TD> <TD valign="top"> V.I. Arnol'd, "Small denominators, I. Mapping the circle onto itself" ''Izv. Akad. Nauk SSSR Ser. Mat.'' , '''25''' : 1 (1961) pp. 21–86 (In Russian)</TD></TR><TR><TD valign="top">[11b]</TD> <TD valign="top"> V.I. Arnol'd, "Correction to "Small denominators, I. Mapping the circle onto itself" " ''Izv. Akad. Nauk SSSR Ser. Mat.'' , '''28''' : 2 (1964) pp. 479–480 (In Russian)</TD></TR><TR><TD valign="top">[12]</TD> <TD valign="top"> C.T.C. Wall, "Geometric properties of generic differentiable manifolds" , ''Geometry and topology'' , ''Lect. notes in math.'' , '''597''' , Springer (1977) pp. 707–774 {{MR|0494233}} {{ZBL|0361.58004}} </TD></TR><TR><TD valign="top">[13]</TD> <TD valign="top"> W. Klingenberg, "Lectures on closed geodesics" , Springer (1978) {{MR|0478069}} {{ZBL|0397.58018}} </TD></TR><TR><TD valign="top">[14]</TD> <TD valign="top"> V.I. Arnol'd, S.M. [S.M. Khusein-Zade] Gusein-Zade, A.N. Varchenko, "Singularities of differentiable maps" , '''1''' , Birkhäuser (1985) (Translated from Russian)</TD></TR><TR><TD valign="top">[15]</TD> <TD valign="top"> V.I. Arnol'd, V.S. Afraimovich, Yu.S. Ilyashenko, L.P. Shil'nikov, "Dynamical systems" , '''5''' , Springer (forthcoming) (Translated from Russian)</TD></TR></table> |
| Line 30: | Line 30: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> R. Thom, "Un lemma sur les applications différentiable" ''Bol. Soc. Math. Mexico'' , '''1''' : 2 (1956) pp. 59–71 {{MR|}} {{ZBL|}} </TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> J.M. Boardman, "Singularities of differentiable maps" ''Publ. Math. IHES'' , '''33''' (1967) pp. 383–419 {{MR|0231390}} {{ZBL|0165.56803}} </TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> Th. Bröcker, "Differentiable germs and catastrophes" , Cambridge Univ. Press (1975) {{MR|0494220}} {{ZBL|0302.58006}} </TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> J.C. Oxtoby, "Measure and category" , Springer (1971) (Translated from German) {{MR|0393403}} {{ZBL|0217.09201}} </TD></TR></table> |
Revision as of 14:49, 24 March 2012
generic position
A term used in such phrases as "the objects O in general (generic) position have the property S (or properties Si)" , "S is a property of general position" , "reduction (transformation) to general position" , the precise meaning of which depends on the context. Usually the set  of all objects considered has a structure allowing certain subsets
of all objects considered has a structure allowing certain subsets  to be regarded as "small" , "negligible" or, conversely, "large" , "massive" ;
to be regarded as "small" , "negligible" or, conversely, "large" , "massive" ;  is then regarded as a "property of general position" if the objects possessing it form a "large" subset of
is then regarded as a "property of general position" if the objects possessing it form a "large" subset of  .
.  usually has one of the following structures: a) an algebraic variety; b) a differentiable manifold (possibly infinite-dimensional); c) a topological space, most often a Baire space in the first meaning of this term; or d) a measure space. The following are considered "small" respectively: algebraic subvarieties (of lower dimension), differentiable submanifolds and finite or countable unions of them, nowhere-dense sets or sets of the first category, sets of measure zero. A set
usually has one of the following structures: a) an algebraic variety; b) a differentiable manifold (possibly infinite-dimensional); c) a topological space, most often a Baire space in the first meaning of this term; or d) a measure space. The following are considered "small" respectively: algebraic subvarieties (of lower dimension), differentiable submanifolds and finite or countable unions of them, nowhere-dense sets or sets of the first category, sets of measure zero. A set  is regarded as "large" if its complement is "small" . One then also says that
is regarded as "large" if its complement is "small" . One then also says that  contains "most" or "almost all" of the objects of
contains "most" or "almost all" of the objects of  , and a property
, and a property  satisfied by almost all objects is called "typical" , or a property of general position. One frequently speaks of a "typical" object, or an object being of general position or an object in general position, implying (sometimes tacitly) that there are one or more "typical" properties (of what kind should be clear from the context) and that one is concerned with an object having these properties.
satisfied by almost all objects is called "typical" , or a property of general position. One frequently speaks of a "typical" object, or an object being of general position or an object in general position, implying (sometimes tacitly) that there are one or more "typical" properties (of what kind should be clear from the context) and that one is concerned with an object having these properties.
In a weaker sense, a "large" subset in cases c) and d) may mean a subset of the second category in a non-empty open subset of the space  or a subset of positive measure. Then one says that this set of objects "cannot be neglected" (but one no longer says that it is "typical" ).
or a subset of positive measure. Then one says that this set of objects "cannot be neglected" (but one no longer says that it is "typical" ).
In cases a) and b) a "small" set 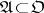 has positive codimension
has positive codimension  . It is natural to say that as
. It is natural to say that as  gets larger,
gets larger, 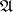 gets smaller. A situation close to b) (but more general) is when one can speak of
gets smaller. A situation close to b) (but more general) is when one can speak of  -parameter families of objects
-parameter families of objects 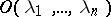 , depending sufficiently smoothly on
, depending sufficiently smoothly on  (scalar) parameters, and when all possible such families form a Baire space. If almost all (in sense c)) of these families do not contain objects of
(scalar) parameters, and when all possible such families form a Baire space. If almost all (in sense c)) of these families do not contain objects of 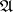 , then one says that
, then one says that  , and if this is true for any
, and if this is true for any  , then one puts
, then one puts  . Considerations of codimension play an important part in bifurcation theory and the theory of singularities of differentiable mappings (see also [8]).
. Considerations of codimension play an important part in bifurcation theory and the theory of singularities of differentiable mappings (see also [8]).
Certain operations 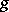 may act on the objects; the set
may act on the objects; the set  of these operations is usually a group, or at least a semi-group with an identity
of these operations is usually a group, or at least a semi-group with an identity  . One speaks of "reduction of an object O to general position by the operation g" when it is clear from the context what properties are being considered; "reduction" means that
. One speaks of "reduction of an object O to general position by the operation g" when it is clear from the context what properties are being considered; "reduction" means that 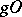 has these properties. Like
has these properties. Like  ,
,  is usually provided with a structure allowing one to speak of a "large" set of operations, or to say that the operation
is usually provided with a structure allowing one to speak of a "large" set of operations, or to say that the operation 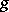 taking
taking  to
to  , with the necessary properties, can be chosen arbitrary close to
, with the necessary properties, can be chosen arbitrary close to  ( "reduction to general position by a small shift" ).
( "reduction to general position by a small shift" ).
For example, a line and a circle in the plane in general position either do not intersect or intersect in two points. In this case the object is the pair 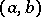 , where
, where  is the line and
is the line and  the circle, and the operations may be taken as Euclidean motions (or just parallel translations), acting on
the circle, and the operations may be taken as Euclidean motions (or just parallel translations), acting on  with
with  fixed. The set of all possible objects
fixed. The set of all possible objects  and the group
and the group  are naturally endowed with the structures mentioned above, and general position can be interpreted according to each of the versions. Originally, the term general position was used in similar geometrical problems, and thence it was transferred to areas of mathematics of a geometrical character, or at least considerably influenced by geometry (although arguments involving sets of the second category or of full measure are used outside these areas). To the present day, the term "general position" is often applied to a situation immediately generalizing the above example, when one speaks of the transversality of two submanifolds in some ambient manifold (or the related situation of transversality of the self-intersections of an immersed submanifold). In particular, in geometric topology (considering piecewise-linear or topological manifolds and the corresponding classes of mappings) the term "general position" is used almost exclusively as a synonym of transversality.
are naturally endowed with the structures mentioned above, and general position can be interpreted according to each of the versions. Originally, the term general position was used in similar geometrical problems, and thence it was transferred to areas of mathematics of a geometrical character, or at least considerably influenced by geometry (although arguments involving sets of the second category or of full measure are used outside these areas). To the present day, the term "general position" is often applied to a situation immediately generalizing the above example, when one speaks of the transversality of two submanifolds in some ambient manifold (or the related situation of transversality of the self-intersections of an immersed submanifold). In particular, in geometric topology (considering piecewise-linear or topological manifolds and the corresponding classes of mappings) the term "general position" is used almost exclusively as a synonym of transversality.
In algebraic geometry simple examples (like the one above) can easily be analyzed by elimination theory, where the ground field may be completely arbitrary (usually algebraically closed). There are theorems on general position in more complicated situations (for example, Bertini theorems, and the Lefschetz theorem on a hyperplane section); in studying the action of algebraic groups on algebraic varieties points in general position (cf. Point in general position) play a large part [1].
In differential topology and the theory of singularities of differentiable mappings, general position is used very extensively. Proofs are usually carried out by means of Sard's theorem or its corollaries, and the Abraham and Thom transversality theorems (see [2], [3]), which are more suitable for immediate application. In the infinite-dimensional case Sard's theorem is not valid, but weaker results that are sometimes sufficient can be obtained (see [4], [5], [14]).
There are several results on "typical" properties in the theory of smooth dynamical systems. Most of them are proved (particularly, in bifurcation theory) by reduction to Sard's theorem; positive results not connected with this reduction are few (see [6], [7], [9], [10], and the references to Rough system). A characteristic of the theory of smooth dynamical systems is the presence of an essential distinction between general position in the topological and metric sense (c) and d) above) , [15].
For general position in the differential geometry of manifolds see [12], [13].
References
| [1] | D. Mumford, "Geometric invariant theory" , Springer (1965) MR0214602 Zbl 0147.39304 |
| [2] | S. Lang, "Introduction to differentiable manifolds" , Interscience (1967) pp. App. III MR1931083 MR1532744 MR0155257 Zbl 1008.57001 Zbl 0103.15101 |
| [3] | V.I. Arnol'd, "Chapitres supplémentaires de la théorie des équations différentielles ordinaires" , MIR (1980) (Translated from Russian) |
| [4] | J. Eells, J. McAlpin, "An approximate Morse–Sard theorem" J. Math. Mech. , 17 : 11 (1968) pp. 1055–1064 MR0226680 Zbl 0159.24901 |
| [5] | F. Quinn, "Transversal approximation on Banach manifolds" S.-S. Chern (ed.) S. Smale (ed.) , Global analysis , Proc. Symp. Pure Math. , 14 , Amer. Math. Soc. (1970) pp. 213–222 MR0264713 Zbl 0206.25705 |
| [6] | C. Gutierrez, "Structural stability of flows on the torus with a cross-cap" Trans. Amer. Math. Soc. , 241 (1978) pp. 311–320 |
| [7] | C. Gutierrez, "Smooth nonorientable nontrivial recurrence on two-manifolds" J. Differential Equations , 29 : 3 (1978) pp. 388–395 MR0507486 Zbl 0413.58018 |
| [8] | H. Kurland, J. Robbin, "Infinite codimension and transversality" A. Manning (ed.) , Dynamical systems (Warwick, 1974) , Lect. notes in math. , 468 , Springer (1975) pp. 135–150 MR0649273 Zbl 0317.58011 |
| [9] | F. Takens, "Tolerance stability" A. Manning (ed.) , Dynamical systems (Warwick, 1974) , Lect. notes in math. , 468 , Springer (1975) pp. 293–304 MR0650298 Zbl 0321.54022 |
| [10] | V.A. Dobrynskii, A.N. Sharkovskii, "Typicalness of dynamical systems almost all paths of which are stable under permanently acting perturbations" Soviet Math. Dokl. , 14 : 4 (1973) pp. 997–1000 Dokl. Akad. Nauk SSSR , 211 : 2 (1973) pp. 273–276 |
| [11a] | V.I. Arnol'd, "Small denominators, I. Mapping the circle onto itself" Izv. Akad. Nauk SSSR Ser. Mat. , 25 : 1 (1961) pp. 21–86 (In Russian) |
| [11b] | V.I. Arnol'd, "Correction to "Small denominators, I. Mapping the circle onto itself" " Izv. Akad. Nauk SSSR Ser. Mat. , 28 : 2 (1964) pp. 479–480 (In Russian) |
| [12] | C.T.C. Wall, "Geometric properties of generic differentiable manifolds" , Geometry and topology , Lect. notes in math. , 597 , Springer (1977) pp. 707–774 MR0494233 Zbl 0361.58004 |
| [13] | W. Klingenberg, "Lectures on closed geodesics" , Springer (1978) MR0478069 Zbl 0397.58018 |
| [14] | V.I. Arnol'd, S.M. [S.M. Khusein-Zade] Gusein-Zade, A.N. Varchenko, "Singularities of differentiable maps" , 1 , Birkhäuser (1985) (Translated from Russian) |
| [15] | V.I. Arnol'd, V.S. Afraimovich, Yu.S. Ilyashenko, L.P. Shil'nikov, "Dynamical systems" , 5 , Springer (forthcoming) (Translated from Russian) |
Comments
For Thom's transversality theorem see Singularities of differentiable mappings and [a1]. In finite dimensions it was generalized to jet extensions [a2]. A simplified proof of the transversality theorem, together with a proof of Sard's theorem (cf. also Sard theorem), can be found, e.g., in [a3].
Finally, in situations where one has several structures (like in  : a topological structure and the Lebesgue measure), the different notions of general position lead to paradoxal examples, see [a4].
: a topological structure and the Lebesgue measure), the different notions of general position lead to paradoxal examples, see [a4].
References
| [a1] | R. Thom, "Un lemma sur les applications différentiable" Bol. Soc. Math. Mexico , 1 : 2 (1956) pp. 59–71 |
| [a2] | J.M. Boardman, "Singularities of differentiable maps" Publ. Math. IHES , 33 (1967) pp. 383–419 MR0231390 Zbl 0165.56803 |
| [a3] | Th. Bröcker, "Differentiable germs and catastrophes" , Cambridge Univ. Press (1975) MR0494220 Zbl 0302.58006 |
| [a4] | J.C. Oxtoby, "Measure and category" , Springer (1971) (Translated from German) MR0393403 Zbl 0217.09201 |
General position. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=General_position&oldid=21869