Difference between revisions of "Character group"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 26: | Line 26: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> A. Borel, "Linear algebraic groups" , Benjamin (1969)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> S.A. Morris, "Pontryagin duality and the structure of locally compact Abelian groups" , ''London Math. Soc. Lecture Notes'' , '''29''' , Cambridge Univ. Press (1977)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> L.S. Pontryagin, "Topological groups" , Princeton Univ. Press (1958) (Translated from Russian)</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> L. Fuchs, "Infinite abelian groups" , '''1''' , Acad. Press (1970)</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> J.E. Humphreys, "Linear algebraic groups" , Springer (1975)</TD></TR></table> | + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> A. Borel, "Linear algebraic groups" , Benjamin (1969) {{MR|0251042}} {{ZBL|0206.49801}} {{ZBL|0186.33201}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> S.A. Morris, "Pontryagin duality and the structure of locally compact Abelian groups" , ''London Math. Soc. Lecture Notes'' , '''29''' , Cambridge Univ. Press (1977) {{MR|0442141}} {{ZBL|0446.22006}} </TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> L.S. Pontryagin, "Topological groups" , Princeton Univ. Press (1958) (Translated from Russian) {{MR|0201557}} {{ZBL|0022.17104}} </TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> L. Fuchs, "Infinite abelian groups" , '''1''' , Acad. Press (1970) {{MR|0255673}} {{ZBL|0209.05503}} </TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> J.E. Humphreys, "Linear algebraic groups" , Springer (1975) {{MR|0396773}} {{ZBL|0325.20039}} </TD></TR></table> |
| Line 38: | Line 38: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> E. Hewitt, K.A. Ross, "Abstract harmonic analysis" , '''1''' , Springer (1963)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> N. Bourbaki, "Elements of mathematics. Spectral theories" , Addison-Wesley (1977) (Translated from French)</TD></TR></table> | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> E. Hewitt, K.A. Ross, "Abstract harmonic analysis" , '''1''' , Springer (1963) {{MR|0156915}} {{ZBL|0115.10603}} </TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> N. Bourbaki, "Elements of mathematics. Spectral theories" , Addison-Wesley (1977) (Translated from French) {{MR|0583191}} {{ZBL|1106.46004}} </TD></TR></table> |
Revision as of 10:02, 24 March 2012
of a group 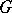
The group 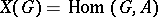 of all characters of
of all characters of 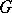 (cf. Character of a group) with values in an Abelian group
(cf. Character of a group) with values in an Abelian group 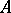 , under the operation
, under the operation
 |
induced by the operation in 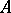 . When
. When 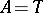 , then
, then
 |
where 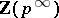 are quasi-cyclic groups, one for each prime number
are quasi-cyclic groups, one for each prime number 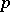 . This group is algebraically compact (see Pure subgroup). If
. This group is algebraically compact (see Pure subgroup). If 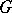 is Abelian, then
is Abelian, then 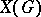 is a divisible group if and only if
is a divisible group if and only if 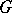 is torsion free and it is a reduced group if and only if
is torsion free and it is a reduced group if and only if 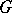 is periodic [4].
is periodic [4].
The character group of a topological group 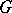 is the group
is the group 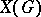 of all continuous homomorphisms
of all continuous homomorphisms 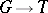 , equipped with the compact-open topology. It is a Hausdorff Abelian topological group. If
, equipped with the compact-open topology. It is a Hausdorff Abelian topological group. If 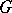 is locally compact, then so is
is locally compact, then so is 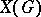 ; if
; if 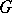 is compact, then
is compact, then 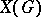 is discrete, and if
is discrete, and if 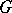 is discrete, then
is discrete, then 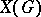 is compact.
is compact.
Examples of character groups:
 |
for any finite discrete Abelian group 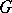 .
.
With every continuous homomorphism of topological groups 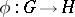 there is associated a homomorphism of the character groups
there is associated a homomorphism of the character groups 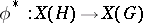 . Here the correspondence
. Here the correspondence 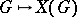 ,
, 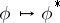 , is a contravariant functor from the category of topological groups into the category of Abelian topological groups. If the category is restricted to locally compact Abelian groups
, is a contravariant functor from the category of topological groups into the category of Abelian topological groups. If the category is restricted to locally compact Abelian groups 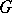 , then this functor determines an equivalence of that category and its dual category (see Pontryagin duality).
, then this functor determines an equivalence of that category and its dual category (see Pontryagin duality).
The character group of an algebraic group 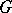 over a field
over a field 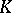 is the group
is the group 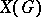 of all rational characters
of all rational characters 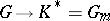 . If
. If 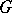 is an Abelian affine algebraic group, then
is an Abelian affine algebraic group, then 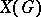 generates the space
generates the space 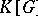 (that is, is a basis in this space) if and only if
(that is, is a basis in this space) if and only if 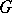 is a diagonalizable algebraic group, i.e. is isomorphic to a closed subgroup of a certain torus
is a diagonalizable algebraic group, i.e. is isomorphic to a closed subgroup of a certain torus 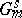 . Here
. Here  is a finitely generated Abelian group (without
is a finitely generated Abelian group (without 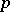 -torsion if
-torsion if 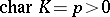 ), and
), and 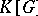 is the group algebra of
is the group algebra of 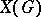 over
over 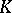 , which makes it possible to define a duality between the categories of diagonalizable groups and that of finitely generated Abelian groups (without
, which makes it possible to define a duality between the categories of diagonalizable groups and that of finitely generated Abelian groups (without 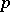 -torsion if
-torsion if 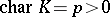 ), cf. [1]. When
), cf. [1]. When 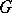 is a finite group (regarded as a
is a finite group (regarded as a  -dimensional algebraic group) and
-dimensional algebraic group) and 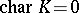 , then this duality is the same as the classical duality of finite Abelian groups.
, then this duality is the same as the classical duality of finite Abelian groups.
For any connected algebraic group 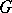 , the group
, the group 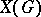 is torsion free. In particular, a diagonalizable group
is torsion free. In particular, a diagonalizable group 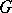 is a torus if and only if
is a torus if and only if 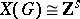 .
.
References
| [1] | A. Borel, "Linear algebraic groups" , Benjamin (1969) MR0251042 Zbl 0206.49801 Zbl 0186.33201 |
| [2] | S.A. Morris, "Pontryagin duality and the structure of locally compact Abelian groups" , London Math. Soc. Lecture Notes , 29 , Cambridge Univ. Press (1977) MR0442141 Zbl 0446.22006 |
| [3] | L.S. Pontryagin, "Topological groups" , Princeton Univ. Press (1958) (Translated from Russian) MR0201557 Zbl 0022.17104 |
| [4] | L. Fuchs, "Infinite abelian groups" , 1 , Acad. Press (1970) MR0255673 Zbl 0209.05503 |
| [5] | J.E. Humphreys, "Linear algebraic groups" , Springer (1975) MR0396773 Zbl 0325.20039 |
Comments
In the article above 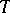 denotes the circle group. A periodic group is also called a torsion group. An Abelian group is reduced if it contains no non-trivial divisible subgroups.
denotes the circle group. A periodic group is also called a torsion group. An Abelian group is reduced if it contains no non-trivial divisible subgroups.
Above, the phrase "character" is of course strictly used in its narrowest meaning of a (continuous) homomorphism 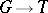 and not in the sense of the character of some representation.
and not in the sense of the character of some representation.
The character groups of many locally Abelian groups can be found in [a1].
References
| [a1] | E. Hewitt, K.A. Ross, "Abstract harmonic analysis" , 1 , Springer (1963) MR0156915 Zbl 0115.10603 |
| [a2] | N. Bourbaki, "Elements of mathematics. Spectral theories" , Addison-Wesley (1977) (Translated from French) MR0583191 Zbl 1106.46004 |
Character group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Character_group&oldid=21823