Difference between revisions of "Markov chain, recurrent"
(Importing text file) |
(MSC|60J10 Category:Markov chains) |
||
| Line 1: | Line 1: | ||
| + | {{MSC|60J10}} | ||
| + | |||
| + | [[Category:Markov chains]] | ||
| + | |||
A [[Markov chain|Markov chain]] in which a random trajectory <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m062/m062430/m0624301.png" />, starting at any state <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m062/m062430/m0624302.png" />, returns to that state with probability 1. In terms of the [[Transition probabilities|transition probabilities]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m062/m062430/m0624303.png" />, recurrence of a discrete-time Markov chain is equivalent to the divergence for any <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m062/m062430/m0624304.png" /> of the series | A [[Markov chain|Markov chain]] in which a random trajectory <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m062/m062430/m0624301.png" />, starting at any state <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m062/m062430/m0624302.png" />, returns to that state with probability 1. In terms of the [[Transition probabilities|transition probabilities]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m062/m062430/m0624303.png" />, recurrence of a discrete-time Markov chain is equivalent to the divergence for any <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m062/m062430/m0624304.png" /> of the series | ||
Revision as of 20:26, 9 March 2012
2020 Mathematics Subject Classification: Primary: 60J10 [MSN][ZBL]
A Markov chain in which a random trajectory 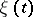 , starting at any state
, starting at any state 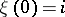 , returns to that state with probability 1. In terms of the transition probabilities
, returns to that state with probability 1. In terms of the transition probabilities 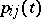 , recurrence of a discrete-time Markov chain is equivalent to the divergence for any
, recurrence of a discrete-time Markov chain is equivalent to the divergence for any 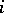 of the series
of the series
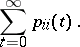 |
In a recurrent Markov chain a trajectory 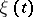 ,
, 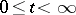 ,
, 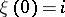 , returns infinitely often to the state
, returns infinitely often to the state 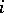 with probability 1. In a recurrent Markov chain there are no inessential states and the essential states decompose into recurrent classes. An example of a recurrent Markov chain is the symmetric random walk on the integer lattice on the line or plane. In the symmetric walk on the line a particle moves from position
with probability 1. In a recurrent Markov chain there are no inessential states and the essential states decompose into recurrent classes. An example of a recurrent Markov chain is the symmetric random walk on the integer lattice on the line or plane. In the symmetric walk on the line a particle moves from position  to
to 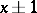 with probabilities
with probabilities 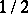 ; in the symmetric walk on the plane a particle moves from
; in the symmetric walk on the plane a particle moves from 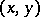 to one of the four points
to one of the four points 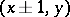 ,
, 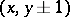 with probabilities
with probabilities 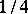 . In these examples a particle, starting the walk at an arbitrary point, returns to that point with probability 1. The symmetric walk on the integer lattice in the three-dimensional space, when the probability of transition from
. In these examples a particle, starting the walk at an arbitrary point, returns to that point with probability 1. The symmetric walk on the integer lattice in the three-dimensional space, when the probability of transition from  to a neighbouring point
to a neighbouring point 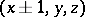 ,
, 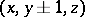 ,
, 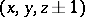 is equal to
is equal to 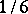 , is not recurrent. In this case the probability of return of the particle to its initial point is approximately 0.35.
, is not recurrent. In this case the probability of return of the particle to its initial point is approximately 0.35.
References
| [1] | W. Feller, "An introduction to probability theory and its applications" , 1 , Wiley (1966) |
Comments
References
| [a1] | D. Freeman, "Markov chains" , Holden-Day (1975) |
| [a2] | M. Iosifescu, "Finite Markov processes and their applications" , Wiley (1980) |
| [a3] | J.G. Kemeny, J.L. Snell, "Finite Markov chains" , v. Nostrand (1960) |
| [a4] | J.G. Kemeny, J.L. Snell, A.W. Knapp, "Denumerable Markov chains" , Springer (1976) |
| [a5] | D. Revuz, "Markov chains" , North-Holland (1975) |
| [a6] | V.I. [V.I. Romanovskii] Romanovsky, "Discrete Markov chains" , Wolters-Noordhoff (1970) (Translated from Russian) |
| [a7] | E. Seneta, "Non-negative matrices and Markov chains" , Springer (1981) |
| [a8] | V. Spitzer, "Principles of random walk" , v. Nostrand (1964) |
Markov chain, recurrent. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Markov_chain,_recurrent&oldid=21655