Difference between revisions of "Geometric distribution"
From Encyclopedia of Mathematics
(Importing text file) |
(MSC|60E99 Category:Distribution theory) |
||
| Line 1: | Line 1: | ||
| + | {{MSC|60E99}} | ||
| + | |||
| + | [[Category:Distribution theory]] | ||
| + | |||
The distribution of a discrete random variable assuming non-negative integral values <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g044/g044230/g0442301.png" /> with probabilities <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g044/g044230/g0442302.png" />, where the distribution parameter <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g044/g044230/g0442303.png" /> is a number in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g044/g044230/g0442304.png" />. The characteristic function is | The distribution of a discrete random variable assuming non-negative integral values <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g044/g044230/g0442301.png" /> with probabilities <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g044/g044230/g0442302.png" />, where the distribution parameter <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g044/g044230/g0442303.png" /> is a number in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g044/g044230/g0442304.png" />. The characteristic function is | ||
Revision as of 17:54, 22 February 2012
2020 Mathematics Subject Classification: Primary: 60E99 [MSN][ZBL]
The distribution of a discrete random variable assuming non-negative integral values 
with probabilities 
, where the distribution parameter 
is a number in 
. The characteristic function is
 |
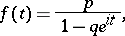the mathematical expectation is 
; the variance is 
; the generating function is
 |
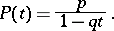Figure: g044230a
A geometric distribution of probability 
.
Figure: g044230b
The distribution function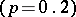 
.
The random variable equal to the number of independent trials prior to the first successful outcome with a probability of success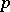 
and a probability of failure 
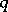has a geometric distribution. The name originates from the geometric progression which generates such a distribution.
How to Cite This Entry:
Geometric distribution. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Geometric_distribution&oldid=21286
Geometric distribution. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Geometric_distribution&oldid=21286
This article was adapted from an original article by V.M. Kalinin (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article