Difference between revisions of "Cramér theorem"
(Undo revision 20876 by Boris Tsirelson (talk) oops) |
(MSC|60F10 Category:Limit theorems (again)) |
||
| Line 1: | Line 1: | ||
| + | {{MSC|60F10}} | ||
| + | |||
| + | [[Category:Limit theorems]] | ||
| + | |||
An integral limit theorem for the probability of large deviations of sums of independent random variables. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c027/c027000/c0270001.png" /> be a sequence of independent random variables with the same non-degenerate distribution function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c027/c027000/c0270002.png" />, such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c027/c027000/c0270003.png" /> and such that the generating function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c027/c027000/c0270004.png" /> of the moments is finite in some interval <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c027/c027000/c0270005.png" /> (this last condition is known as the Cramér condition). Let | An integral limit theorem for the probability of large deviations of sums of independent random variables. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c027/c027000/c0270001.png" /> be a sequence of independent random variables with the same non-degenerate distribution function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c027/c027000/c0270002.png" />, such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c027/c027000/c0270003.png" /> and such that the generating function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c027/c027000/c0270004.png" /> of the moments is finite in some interval <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c027/c027000/c0270005.png" /> (this last condition is known as the Cramér condition). Let | ||
Revision as of 19:23, 7 February 2012
2020 Mathematics Subject Classification: Primary: 60F10 [MSN][ZBL]
An integral limit theorem for the probability of large deviations of sums of independent random variables. Let 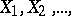 be a sequence of independent random variables with the same non-degenerate distribution function
be a sequence of independent random variables with the same non-degenerate distribution function 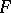 , such that
, such that 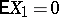 and such that the generating function
and such that the generating function 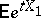 of the moments is finite in some interval
of the moments is finite in some interval 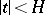 (this last condition is known as the Cramér condition). Let
(this last condition is known as the Cramér condition). Let
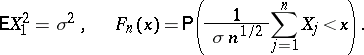 |
If 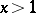 ,
,  as
as 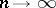 , then
, then
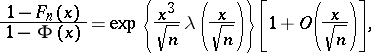 |
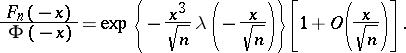 |
Here 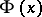 is the normal
is the normal 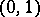 distribution function and
distribution function and 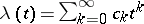 is the so-called Cramér series, the coefficients of which depend only on the moments of the random variable
is the so-called Cramér series, the coefficients of which depend only on the moments of the random variable 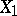 ; this series is convergent for all sufficiently small
; this series is convergent for all sufficiently small 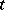 . Actually, the original result, obtained by H. Cramér in 1938, was somewhat weaker than that just described.
. Actually, the original result, obtained by H. Cramér in 1938, was somewhat weaker than that just described.
References
| [1] | H. Cramér, "Sur un nouveau théorème-limite de la théorie des probabilités" , Act. Sci. et Ind. , 736 , Hermann (1938) |
| [2] | I.A. Ibragimov, Yu.V. Linnik, "Independent and stationary sequences of random variables" , Wolters-Noordhoff (1971) (Translated from Russian) |
| [3] | V.V. Petrov, "Sums of independent random variables" , Springer (1975) (Translated from Russian) |
Comments
See also Limit theorems; Probability of large deviations.
References
| [a1] | R.S. Ellis, "Entropy, large deviations, and statistical mechanics" , Springer (1985) |
Cramér theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Cram%C3%A9r_theorem&oldid=20884