Difference between revisions of "Baire set"
From Encyclopedia of Mathematics
(category, MSC) |
(better MSC template) |
||
| Line 1: | Line 1: | ||
''in a locally compact Hausdorff space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b015/b015050/b0150501.png" />'' | ''in a locally compact Hausdorff space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b015/b015050/b0150501.png" />'' | ||
| + | |||
| + | {{MSC|28A05|03E15,54H05}} | ||
[[Category:Classical measure theory]] | [[Category:Classical measure theory]] | ||
| − | |||
| − | |||
A set belonging to the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b015/b015050/b0150502.png" />-ring generated by the class of all compact sets in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b015/b015050/b0150503.png" /> that are <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b015/b015050/b0150504.png" />-sets. A Baire set serves to define the concept of a Baire-measurable function. In all classical particular cases in which measure theory is developed in topological spaces, e.g. in Euclidean spaces, the concept of a Baire set coincides with that of a [[Borel set|Borel set]]. | A set belonging to the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b015/b015050/b0150502.png" />-ring generated by the class of all compact sets in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b015/b015050/b0150503.png" /> that are <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b015/b015050/b0150504.png" />-sets. A Baire set serves to define the concept of a Baire-measurable function. In all classical particular cases in which measure theory is developed in topological spaces, e.g. in Euclidean spaces, the concept of a Baire set coincides with that of a [[Borel set|Borel set]]. | ||
Revision as of 16:03, 28 January 2012
in a locally compact Hausdorff space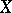 
2020 Mathematics Subject Classification: Primary: 28A05 Secondary: 03E1554H05 [MSN][ZBL]
A set belonging to the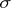 
-ring generated by the class of all compact sets in 
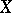that are 
-sets. A Baire set serves to define the concept of a Baire-measurable function. In all classical particular cases in which measure theory is developed in topological spaces, e.g. in Euclidean spaces, the concept of a Baire set coincides with that of a Borel set.
References
| [1] | P.R. Halmos, "Measure theory" , v. Nostrand (1950) |
How to Cite This Entry:
Baire set. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Baire_set&oldid=20663
Baire set. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Baire_set&oldid=20663
This article was adapted from an original article by V.A. Skvortsov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article