Difference between revisions of "User:Rafael.greenblatt/sandbox"
| Line 1: | Line 1: | ||
| − | (starting to modify "Exterior algebra") | + | (starting to modify "[[Exterior algebra]]") |
| Line 16: | Line 16: | ||
The exterior algebra does not depend on the choice of the basis and is denoted by $\wedge V$. The subspace $\wedge^r V$ ($r=0,1,\ldots$) in $\wedge V$ generated by the elements of the form $e_{i_1} \wedge \ldots \wedge e_{i_r}$ is said to be the $r$-th exterior power of the space $V$. The following equalities are valid: $ \dim \wedge^r V = () = C_n^r$, $r=0,\ldots,n$, $\wedge^r V =0$, $r>n$. In addition, $v \wedge u = (-1)^{rs}u \wedge v$ if $u \in \wedge^r V$, $v \in \wedge^s V$. The elements of the space $\wedge^r V$ are said to be $r$-vectors; they may also be regarded as skew-symmetric $r$-times contravariant tensors in $V$ (cf. [[Exterior product|Exterior product]]). | The exterior algebra does not depend on the choice of the basis and is denoted by $\wedge V$. The subspace $\wedge^r V$ ($r=0,1,\ldots$) in $\wedge V$ generated by the elements of the form $e_{i_1} \wedge \ldots \wedge e_{i_r}$ is said to be the $r$-th exterior power of the space $V$. The following equalities are valid: $ \dim \wedge^r V = () = C_n^r$, $r=0,\ldots,n$, $\wedge^r V =0$, $r>n$. In addition, $v \wedge u = (-1)^{rs}u \wedge v$ if $u \in \wedge^r V$, $v \in \wedge^s V$. The elements of the space $\wedge^r V$ are said to be $r$-vectors; they may also be regarded as skew-symmetric $r$-times contravariant tensors in $V$ (cf. [[Exterior product|Exterior product]]). | ||
| − | $r$-vectors are closely connected with $r$-dimensional subspaces in $V$: Linearly independent systems of vectors $x_1,\ldots,x_r$ and | + | $r$-vectors are closely connected with $r$-dimensional subspaces in $V$: Linearly independent systems of vectors $x_1,\ldots,x_r$ and $y_1,\ldots,y_r$ of $V$ generate the same subspace if and only if the $r$-vectors $x_1\wedge \ldots \wedge x_r$ and $y_1\wedge \ldots \wedge y_r$ are proportional. This fact served as one of the starting points in the studies of H. Grassmann [[#References|[1]]], who introduced exterior algebras as the algebraic apparatus to describe the generation of multi-dimensional subspaces by one-dimensional subspaces. The theory of determinants is readily constructed with the aid of exterior algebras. An exterior algebra may also be defined for more general objects, viz. for unitary modules $M$ over a commutative ring $A$ with identity [[#References|[4]]]. The $r$-th exterior power $\wedge^r M$, $r>0$, of a module $M$ is defined as the quotient module of the $r$-th tensor power of this module by the submodule generated by the elements of the form $x1 \otimes \ldots \otimes x_r$, where $x_i \in M$ and $x_j=x_k$ for certain $j \ne k$. The exterior algebra for $M$ is defined as the direct sum $\wedge M = \bigoplus_{r \ge 0}\wedge^r M$, where $\wedge^0 M = A$, with the naturally introduced multiplication. In the case of a finite-dimensional vector space this definition and the original definition are identical. The exterior algebra of a module is employed in the theory of modules over a principal ideal ring [[#References|[5]]]. |
| − | |||
| − | The Grassmann (or Plücker) coordinates of an | + | The Grassmann (or Plücker) coordinates of an $r$-dimensional subspace $L$ in an $n$-dimensional space $V$ over $k$ are defined as the coordinates of the $r$-vector in $V$ corresponding to $L$, which is defined up to proportionality. Grassmann coordinates may be used to naturally imbed the set of all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e037/e037080/e03708061.png" />-dimensional subspaces in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e037/e037080/e03708062.png" /> into the projective space of dimension <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e037/e037080/e03708063.png" />, where it forms an algebraic variety (called the [[Grassmann manifold|Grassmann manifold]]). Thus one gets several important examples of projective algebraic varieties [[#References|[6]]]. |
Exterior algebras are employed in the calculus of exterior differential forms (cf. [[Differential form|Differential form]]) as one of the basic formalisms in differential geometry [[#References|[7]]], [[#References|[8]]]. Many important results in algebraic topology are formulated in terms of exterior algebras. | Exterior algebras are employed in the calculus of exterior differential forms (cf. [[Differential form|Differential form]]) as one of the basic formalisms in differential geometry [[#References|[7]]], [[#References|[8]]]. Many important results in algebraic topology are formulated in terms of exterior algebras. | ||
Latest revision as of 15:57, 25 January 2012
(starting to modify "Exterior algebra")
Grassmann algebra, of a vector space $V$ over a field $k$
An associative algebra over $k$, the operation in which is denoted by the symbol $\wedge$, with generating elements $1,e_1,\ldots,e_n$ where $e_1,\ldots,e_n$ is a basis of $V$, and with defining relations
$$ e_i \wedge e_j = - e_j \wedge e_i \qquad (i,j=1,\ldots,n), \qquad e_i \wedge e_i = 0, $$
$$ 1 \wedge e_i = e_i \wedge 1 = e_i \qquad (i=1,\ldots,n), \qquad \ \wedge 1 = 1. $$
The exterior algebra does not depend on the choice of the basis and is denoted by $\wedge V$. The subspace $\wedge^r V$ ($r=0,1,\ldots$) in $\wedge V$ generated by the elements of the form $e_{i_1} \wedge \ldots \wedge e_{i_r}$ is said to be the $r$-th exterior power of the space $V$. The following equalities are valid: $ \dim \wedge^r V = () = C_n^r$, $r=0,\ldots,n$, $\wedge^r V =0$, $r>n$. In addition, $v \wedge u = (-1)^{rs}u \wedge v$ if $u \in \wedge^r V$, $v \in \wedge^s V$. The elements of the space $\wedge^r V$ are said to be $r$-vectors; they may also be regarded as skew-symmetric $r$-times contravariant tensors in $V$ (cf. Exterior product).
$r$-vectors are closely connected with $r$-dimensional subspaces in $V$: Linearly independent systems of vectors $x_1,\ldots,x_r$ and $y_1,\ldots,y_r$ of $V$ generate the same subspace if and only if the $r$-vectors $x_1\wedge \ldots \wedge x_r$ and $y_1\wedge \ldots \wedge y_r$ are proportional. This fact served as one of the starting points in the studies of H. Grassmann [1], who introduced exterior algebras as the algebraic apparatus to describe the generation of multi-dimensional subspaces by one-dimensional subspaces. The theory of determinants is readily constructed with the aid of exterior algebras. An exterior algebra may also be defined for more general objects, viz. for unitary modules $M$ over a commutative ring $A$ with identity [4]. The $r$-th exterior power $\wedge^r M$, $r>0$, of a module $M$ is defined as the quotient module of the $r$-th tensor power of this module by the submodule generated by the elements of the form $x1 \otimes \ldots \otimes x_r$, where $x_i \in M$ and $x_j=x_k$ for certain $j \ne k$. The exterior algebra for $M$ is defined as the direct sum $\wedge M = \bigoplus_{r \ge 0}\wedge^r M$, where $\wedge^0 M = A$, with the naturally introduced multiplication. In the case of a finite-dimensional vector space this definition and the original definition are identical. The exterior algebra of a module is employed in the theory of modules over a principal ideal ring [5].
The Grassmann (or Plücker) coordinates of an $r$-dimensional subspace $L$ in an $n$-dimensional space $V$ over $k$ are defined as the coordinates of the $r$-vector in $V$ corresponding to $L$, which is defined up to proportionality. Grassmann coordinates may be used to naturally imbed the set of all  -dimensional subspaces in
-dimensional subspaces in 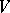 into the projective space of dimension
into the projective space of dimension 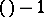 , where it forms an algebraic variety (called the Grassmann manifold). Thus one gets several important examples of projective algebraic varieties [6].
, where it forms an algebraic variety (called the Grassmann manifold). Thus one gets several important examples of projective algebraic varieties [6].
Exterior algebras are employed in the calculus of exterior differential forms (cf. Differential form) as one of the basic formalisms in differential geometry [7], [8]. Many important results in algebraic topology are formulated in terms of exterior algebras.
E.g., if 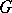 is a finite-dimensional
is a finite-dimensional 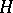 -space (e.g. a Lie group), the cohomology algebra
-space (e.g. a Lie group), the cohomology algebra 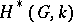 of
of 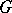 with coefficients in a field
with coefficients in a field 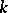 of characteristic zero is an exterior algebra with odd-degree generators. If
of characteristic zero is an exterior algebra with odd-degree generators. If 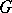 is a simply-connected compact Lie group, then the ring
is a simply-connected compact Lie group, then the ring 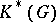 , studied in
, studied in 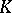 -theory, is also an exterior algebra (over the ring of integers).
-theory, is also an exterior algebra (over the ring of integers).
References
| [1] | H. Grassmann, "Gesammelte mathematische und physikalische Werke" , 1 , Teubner (1894–1896) pp. Chapt. 1; 2 |
| [2] | A.I. Mal'tsev, "Foundations of linear algebra" , Freeman (1963) (Translated from Russian) |
| [3] | L.A. Kaluzhnin, "Introduction to general algebra" , Moscow (1973) (In Russian) |
| [4] | N. Bourbaki, "Elements of mathematics. Algebra: Multilinear algebra" , Addison-Wesley (1966) pp. Chapt. 2 (Translated from French) |
| [5] | N. Bourbaki, "Elements of mathematics. Algebra: Modules. Rings. Forms" , 2 , Addison-Wesley (1975) pp. Chapt.4;5;6 (Translated from French) |
| [6] | W.V.D. Hodge, D. Pedoe, "Methods of algebraic geometry" , 1–3 , Cambridge Univ. Press (1947–1954) |
| [7] | S.P. Finikov, "Cartan's method of exterior forms in differential geometry" , 1–3 , Moscow-Leningrad (1948) (In Russian) |
| [8] | S. Sternberg, "Lectures on differential geometry" , Prentice-Hall (1964) |
Comments
Anticommuting variables (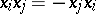 ,
, 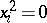 ) are sometimes called Grassmann variables; especially in the context of superalgebras, super-manifolds, etc. (cf. Super-manifold; Superalgebra). In addition the phrase fermionic variables occurs; especially in theoretical physics.
) are sometimes called Grassmann variables; especially in the context of superalgebras, super-manifolds, etc. (cf. Super-manifold; Superalgebra). In addition the phrase fermionic variables occurs; especially in theoretical physics.
References
| [a1] | C. Chevalley, "The construction and study of certain important algebras" , Math. Soc. Japan (1955) |
Rafael.greenblatt/sandbox. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Rafael.greenblatt/sandbox&oldid=20503