Difference between revisions of "Birkhoff ergodic theorem"
(Importing text file) |
(category, MSC) |
||
| Line 1: | Line 1: | ||
| + | [[Category:Ergodic theorems, spectral theory, Markov operators]] | ||
| + | |||
| + | {{User:Rehmann/sandbox/MSC|37A30|37A05,37A10}} | ||
| + | |||
One of the most important theorems in [[Ergodic theory|ergodic theory]]. For an endomorphism <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016530/b0165301.png" /> of a space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016530/b0165302.png" /> with a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016530/b0165303.png" />-finite measure <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016530/b0165304.png" /> Birkhoff's ergodic theorem states that for any function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016530/b0165305.png" /> the limit | One of the most important theorems in [[Ergodic theory|ergodic theory]]. For an endomorphism <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016530/b0165301.png" /> of a space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016530/b0165302.png" /> with a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016530/b0165303.png" />-finite measure <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016530/b0165304.png" /> Birkhoff's ergodic theorem states that for any function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016530/b0165305.png" /> the limit | ||
Revision as of 19:17, 15 January 2012
[ 2010 Mathematics Subject Classification MSN: 37A30,(37A05,37A10) | MSCwiki: 37A30 + 37A05,37A10 ]
One of the most important theorems in ergodic theory. For an endomorphism  of a space
of a space  with a
with a  -finite measure
-finite measure  Birkhoff's ergodic theorem states that for any function
Birkhoff's ergodic theorem states that for any function  the limit
the limit
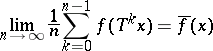 |
(the time average or the average along a trajectory) exists almost everywhere (for almost all  ). Moreover,
). Moreover,  , and if
, and if  , then
, then
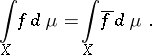 |
For a measurable flow 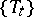 in the space
in the space 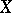 with a
with a 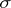 -finite measure
-finite measure  Birkhoff's ergodic theorem states that for any function
Birkhoff's ergodic theorem states that for any function 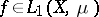 the limit
the limit
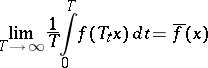 |
exists almost everywhere, with the same properties of 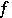 .
.
Birkhoff's theorem was stated and proved by G.D. Birkhoff [1]. It was then modified and generalized in various ways (there are theorems which contain, in addition to Birkhoff's theorem, also a number of statements of a somewhat different kind which are known in probability theory as ergodic theorems (cf. Ergodic theorem); there also exist ergodic theorems for more general semi-groups of transformations [2]). Birkhoff's ergodic theorem and its generalizations are known as individual ergodic theorems, since they deal with the existence of averages along almost each individual trajectory, as distinct from statistical ergodic theorems — the von Neumann ergodic theorem and its generalizations. (In non-Soviet literature the term "pointwise ergodic theorempointwise ergodic theorem" is often used to stress the fact that the averages are almost-everywhere convergent.)
References
| [1] | G.D. Birkhoff, "Proof of the ergodic theorem" Proc. Nat. Acad. Sci. USA , 17 (1931) pp. 656–660 |
| [2] | A.B. Katok, Ya.G. Sinai, A.M. Stepin, "Theory of dynamical systems and general transformation groups with invariant measure" J. Soviet Math. , 7 : 6 (1977) pp. 974–1065 Itogi Nauk. i Tekhn. Mat. Analiz , 13 (1975) pp. 129–262 |
Comments
In non-Soviet literature, the term mean ergodic theorem is used instead of "statistical ergodic theorem" .
A comprehensive overview of ergodic theorems is in [a1]. Many books on ergodic theory contain full proofs of (one or more) ergodic theorems; see e.g. [a2].
References
| [a1] | U. Krengel, "Ergodic theorems" , de Gruyter (1985) |
| [a2] | K. Peterson, "Ergodic theory" , Cambridge Univ. Press (1983) |
Birkhoff ergodic theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Birkhoff_ergodic_theorem&oldid=20304