Difference between revisions of "Arcsine distribution"
(Importing text file) |
(60E99; Category:Distribution theory) |
||
| Line 1: | Line 1: | ||
| + | {{User:Rehmann/sandbox/MSC|60E99|}} | ||
| + | |||
A [[Probability measure|probability measure]] on the real line whose density is zero outside the interval <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a013/a013160/a0131601.png" /> and is <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a013/a013160/a0131602.png" /> if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a013/a013160/a0131603.png" />. The corresponding distribution function is equal to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a013/a013160/a0131604.png" /> for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a013/a013160/a0131605.png" />. | A [[Probability measure|probability measure]] on the real line whose density is zero outside the interval <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a013/a013160/a0131601.png" /> and is <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a013/a013160/a0131602.png" /> if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a013/a013160/a0131603.png" />. The corresponding distribution function is equal to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a013/a013160/a0131604.png" /> for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a013/a013160/a0131605.png" />. | ||
| Line 9: | Line 11: | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> W. Feller, "An introduction to probability theory and its applications" , '''1–2''' , Wiley (1957–1971)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> M.G. Kendall, A. Stuart, "The advanced theory of statistics. Distribution theory" , '''3. Design and analysis''' , Griffin (1969)</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> W. Feller, "An introduction to probability theory and its applications" , '''1–2''' , Wiley (1957–1971)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> M.G. Kendall, A. Stuart, "The advanced theory of statistics. Distribution theory" , '''3. Design and analysis''' , Griffin (1969)</TD></TR></table> | ||
| + | |||
| + | [[Category:Distribution theory]] | ||
Revision as of 15:42, 7 January 2012
[ 2010 Mathematics Subject Classification MSN: 60E99 | MSCwiki: 60E99 ]
A probability measure on the real line whose density is zero outside the interval 
and is 
if 
. The corresponding distribution function is equal to 
for 
.
The generalized arcsine distribution is employed together with the arcsine distribution. To the generalized arcsine distribution corresponds the distribution function 
with density
 |
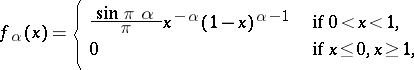if 
. The density 
coincides with the density of the arcsine distribution. The generalized arcsine distribution is a special case of the beta-distribution. The first-order moment of the generalized arcsine distribution is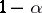 
, and its variance is 
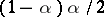. The arcsine distribution and the generalized arcsine distribution occur in the study of the fluctuations of random walks, in renewal theory (cf. Arcsine law), and are used in mathematical statistics as special cases of the beta-distribution.
References
| [1] | W. Feller, "An introduction to probability theory and its applications" , 1–2 , Wiley (1957–1971) |
| [2] | M.G. Kendall, A. Stuart, "The advanced theory of statistics. Distribution theory" , 3. Design and analysis , Griffin (1969) |
Arcsine distribution. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Arcsine_distribution&oldid=20047