Pythagorean theorem

Also known as Pythagoras' theorem, the Pythagorean theorem is a theorem in geometry that gives a relationship between the sides of a right-angled triangle. The Pythagorean theorem was evidently known before Pythagoras (6th century B.C.), but the proof in general form is ascribed to him. Originally the theorem established a relationship between the areas of the squares constructed on the sides of a right-angled triangle: The square on the hypotenuse is equal to the sum of the squares on the other sides. Sometimes, the Pythagorean theorem is formulated briefly as follows: The square of the hypotenuse of a right-angled triangle is equal to the sum of the squares of the catheti. The theorem converse to the Pythagorean theorem is also true: If the square of a side of a triangle is equal to the sum of the squares of the other two sides, then that triangle is right-angled.

Comments

The Pythagorean theorem is a special case of the cosine theorem; its infinite-dimensional analogue (in Hilbert space) is the Parseval equality (i.e. the completeness theorem for orthonormal systems).

The problem of solving Phytagoras' equation $a^2+b^2=c^2$ in integers leads to the Pythagorean numbers. The problem of solving its generalization, the Diophantine equation 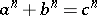, , 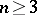is called Fermat's last (or great) theorem, cf. Fermat great theorem.

A right-angled triangle with sides having integer lengths is called a Phytagorean triangle.

References

[a1]	W.H. Greub, "Linear algebra" , Springer (1967)