Difference between revisions of "Pythagorean theorem"
(Importing text file) |
m (moved Pythagoras theorem to Pythagoras' theorem: Titled incorrectly) |
(No difference)
| |
Revision as of 05:57, 28 March 2011
A theorem in geometry that gives a relationship between the sides of a right-angled triangle. Pythagoras' theorem was evidently known before Pythagoras (6th century B.C.), but the proof in general form is ascribed to him. Originally the theorem established a relationship between the areas of the squares constructed on the sides of a right-angled triangle: The square on the hypotenuse is equal to the sum of the squares on the other sides. Sometimes, Pythagoras' theorem is formulated briefly as follows: The square of the hypotenuse of a right-angled triangle is equal to the sum of the squares of the catheti. The theorem converse to Pythagoras' theorem is also true: If the square of a side of a triangle is equal to the sum of the squares of the other two sides, then that triangle is right-angled.
Comments
Phytagoras' theorem is a special case of the cosine theorem; its infinite-dimensional analogue (in Hilbert space) is the Parseval equality (i.e. the completeness theorem for orthonormal systems).
The problem of solving Phytagoras' equation  in integers
in integers  leads to the Pythagorean numbers. The problem of solving its generalization, the Diophantine equation
leads to the Pythagorean numbers. The problem of solving its generalization, the Diophantine equation 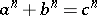 ,
,  , is called Fermat's last (or great) theorem, cf. Fermat great theorem.
, is called Fermat's last (or great) theorem, cf. Fermat great theorem.
A right-angled triangle with sides having integer lengths is called a Phytagorean triangle.
References
| [a1] | W.H. Greub, "Linear algebra" , Springer (1967) |
Pythagorean theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Pythagorean_theorem&oldid=19342