Difference between revisions of "Broyden method"
m (AUTOMATIC EDIT (latexlist): Replaced 91 formulas out of 93 by TEX code with an average confidence of 2.0 and a minimal confidence of 2.0.) |
m (Automatically changed introduction) |
||
| Line 2: | Line 2: | ||
the semi-automatic procedure described at https://encyclopediaofmath.org/wiki/User:Maximilian_Janisch/latexlist | the semi-automatic procedure described at https://encyclopediaofmath.org/wiki/User:Maximilian_Janisch/latexlist | ||
was used. | was used. | ||
| − | If the TeX and formula formatting is correct, please remove this message and the {{TEX|semi-auto}} category. | + | If the TeX and formula formatting is correct and if all png images have been replaced by TeX code, please remove this message and the {{TEX|semi-auto}} category. |
Out of 93 formulas, 91 were replaced by TEX code.--> | Out of 93 formulas, 91 were replaced by TEX code.--> | ||
| − | {{TEX|semi-auto}}{{TEX| | + | {{TEX|semi-auto}}{{TEX|part}} |
An iterative algorithm for solving non-linear equations. The equation to be solved is | An iterative algorithm for solving non-linear equations. The equation to be solved is | ||
Latest revision as of 17:43, 1 July 2020
An iterative algorithm for solving non-linear equations. The equation to be solved is
\begin{equation} \tag{a1} F ( x ) = 0, \end{equation}
where $F : \mathbf{R} ^ { N } \rightarrow \mathbf{R} ^ { N }$ is Lipschitz continuously differentiable (cf. also Lipschitz condition). Let $F ^ { \prime }$ be the Jacobian of $F$.
Here, the setting is such that linear equations can be solved by direct methods and hence it is assumed that $N$ is not very large or that special structure is present that permits efficient sparse matrix factorizations. Having said that, however, note that Broyden's method can be effective on certain very large problems [a14] having dense and very large Jacobians.
Convergence properties.
The Newton method updates a current approximation $x _ { c }$ to a solution $x ^ { * }$ by
\begin{equation} \tag{a2} x _ { + } = x _ { c } - F ^ { \prime } ( x _ { c } ) ^ { - 1 } F ( x _ { c } ). \end{equation}
When a method is specified in terms of the $( x _ { c } , x _ { + } )$-notation, it is understood that the iteration follows the rule with $x _ { n }$ playing the role of $x _ { c }$ and $x_{n+1}$ that of $x_{+}$. The classic local convergence theory for Newton's method, [a4], [a13], [a7] states that if the initial iterate $x _ { 0 }$ is sufficiently near $x ^ { * }$ and $F ^ { \prime } ( x ^ { * } )$ is non-singular, then the Newton iteration converges $q$-quadratically to $x ^ { * }$. This means that
\begin{equation} \tag{a3} \| x _ { n + 1} - x ^ { * } \| = O ( \| x _ { n } - x ^ { * } \| ^ { 2 } ), \end{equation}
hence the number of significant figures roughly doubles with each iteration.
The cost of implementation in Newton's method is both in evaluations of functions and Jacobians and in the matrix factorization required to solve the equation for the Newton step
\begin{equation} \tag{a4} F ^ { \prime } ( x _ { c } ) s = - F ( x _ { c } ), \end{equation}
which is an implicit part of (a2). One way to reduce the cost of forming and factoring a Jacobian is to do this only for the initial iterate and amortize the cost over the entire iteration. The resulting method is called the chord method:
\begin{equation} \tag{a5} x _ { + } = x _ { c } - F ^ { \prime } ( x _ { 0 } ) ^ { - 1 } F ( x _ { c } ). \end{equation}
The chord method will converge rapidly, although not as rapidly as Newton's method, if the initial iterate is sufficiently near $x ^ { * }$ and $F ^ { \prime } ( x ^ { * } )$ is non-singular. The chord iterates satisfy
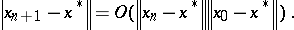 | (a6) |
The convergence implied by (a6) is fast if $x _ { 0 }$ is a very good approximation to $x ^ { * }$, and in such a case the chord method is recommended. The chord iteration can be quite slow or diverge completely even in cases where $x _ { 0 }$ is accurate enough for Newton's method to perform well and converge $q$-quadratically.
Quasi-Newton methods (cf. also Quasi-Newton method) update both an approximation to $x ^ { * }$ and one to $F ^ { \prime } ( x ^ { * } )$. The simplest of these is Broyden's method, [a1]. If $x _ { c }$ and $B _ { c }$ are the current approximations to the $x ^ { * }$ and $F ^ { \prime } ( x ^ { * } )$, then, similarly to Newton's method and the chord method,
\begin{equation} \tag{a7} x _ { + } = x _ { c } - B _ { c } ^ { - 1 } F ( x _ { c } ). \end{equation}
The approximate Jacobian is updated with a rank-one transformation
\begin{equation} \tag{a8} B _ { + } = B _ { c } + \frac { ( y - B _ { c } s ) s ^ { T } } { s ^ { T } s }. \end{equation}
In (a8), $y = F ( x _ { + } ) - F ( x _ { c } )$ and $s = x _ { + } - x _ { c }$.
In the case of a scalar equation $f ( x ) = 0$, $N = 1$ and Broyden's method is the well-known secant method
\begin{equation*} b _ { n + 1 } = \frac { f ( x _ { n + 1} ) - f ( x _ { n } ) } { x _ { n + 1} - x _ { n } }. \end{equation*}
The convergence behaviour, [a3], [a2], lies in between (a3) and (a6). If $x _ { 0 }$ and $B_0$ are sufficiently near $x ^ { * }$ and $F ^ { \prime } ( x ^ { * } )$ and $F ^ { \prime } ( x ^ { * } )$ is non-singular, then either $x _ { n } = x ^ { * }$ for some finite $n$ or $x _ { n } \rightarrow x ^ { * }$ $q$-superlinearly:
\begin{equation} \tag{a9} \operatorname { lim } _ { n \rightarrow \infty } \frac { \left\| x _ { n + 1} - x ^ { * } \right\| } { \left\| x _ { n } - x ^ { * } \right\| } = 0. \end{equation}
If $F ^ { \prime } ( x ^ { * } )$ is singular, Newton's method and Broyden's method (but not the chord method) will still converge at an acceptable rate in many circumstances, [a10], [a11], [a12].
Implementation.
The simple implementation from [a6], described below, is based directly on an approximation of the inverse of the Jacobian. The approach is based on a simple formula, [a8], [a9]. If $B$ is a non-singular $( N \times N )$-matrix and $u , v \in {\bf R} ^ { N }$, then $B + u v ^ { T }$ is invertible if and only if $1 + v ^ { T } B ^ { - 1 } u \neq 0$. In this case
\begin{equation} \tag{a10} ( B + u v ^ { T } ) ^ { - 1 } = \left( I - \frac { ( B ^ { - 1 } u ) v ^ { T } } { 1 + v ^ { T } B ^ { - 1 } u } \right) B ^ { - 1 }. \end{equation}
The formula (a10) is called the Sherman–Morrison formula.
To start with, note that it can be assumed that $B _ { 0 } = I$. The reason for this is that if $B_0$ is a good approximation to $F ^ { \prime } ( x ^ { * } )$, then one may equally well apply Broyden's method to $G ( x ) = 0$ with $G = B _ { 0 } ^ { - 1 } F ( x )$ and use the identity matrix as an approximation to $G ^ { \prime } ( x ^ { * } )$. One way to do this is to form and factor $F ^ { \prime } ( x _ { 0 } )$ and replace $F$ by $G ( x ) = F ^ { \prime } ( x _ { 0 } ) ^ { - 1 } F ( x )$. In this way, just like the chord method, the computation and factorization of $F ^ { \prime } ( x _ { 0 } )$ is amortized over the entire iteration, but one also gets the faster convergence and enhanced robustness of Broyden's method.
In the context of a sequence of Broyden updates $\{ B _ { n } \}$, for $n \geq 0$ one has
\begin{equation*} B _ { n + 1 } = B _ { n } + u _ { n } v _ { n } ^ { T }, \end{equation*}
where
\begin{equation*} u _ { n } = \frac { y _ { n } } { \| s _ { n } \| _ { 2 } } \text { and } v _ { n } = \frac { s _ { n } } { \| s _ { n } \| _ { 2 } }. \end{equation*}
Setting
\begin{equation*} w _ { n } = \frac { B _ { n } ^ { - 1 } u _ { n } } { 1 + v _ { n } ^ { T } B _ { n } ^ { - 1 } u _ { n } }, \end{equation*}
one sees that
\begin{equation} \tag{a11} B _ { n } ^ { - 1 } = \prod _ { j = 0 } ^ { n - 1 } ( I - w _ { j } v _ { j } ^ { T } ) B _ { 0 } ^ { - 1 }. \end{equation}
Since the empty matrix product is the identity, (a11) is valid for $n \geq 0$.
Hence the action of $B _ { n } ^ { - 1 }$ on $F ( x _ { n } )$ (i.e., the computation of the Broyden step) can be computed from the $2 n$ vectors $\{ w _ { j } , v _ { j } \} _ { j = 0 } ^ { n - 1 }$ at a cost of $O ( N n )$ floating point operations. Moreover, the Broyden step for the following iteration is
\begin{equation} \tag{a12} s _ { n } = - B _ { n } ^ { - 1 } F ( x _ { n } ) = \end{equation}
\begin{equation*} = - \prod _ { j = 0 } ^ { n - 1 } ( I - w _ { j } v _ { j } ^ { T } ) B _ { 0 } ^ { - 1 } F ( x _ { n } ). \end{equation*}
Since the product
\begin{equation*} \prod _ { j = 0 } ^ { n - 2 } ( I - w _ { j } v _ { j } ^ { T } ) B _ { 0 } ^ { - 1 } F ( x _ { n } ) \end{equation*}
must also be computed as part of the computation of $w _ { n - 1}$, one can combine the computation of $w _ { n - 1}$ and $s _ { n }$ as follows:
\begin{equation} \tag{a13} w = \prod _ { j = 0 } ^ { n - 2 } ( I - w _ { j } v _ { j } ^ { T } ) B _ { 0 } ^ { - 1 } F ( x _ { n } ), \end{equation}
\begin{equation*} w _ { n - 1 } = ( \| s _ { n - 1} \| _ { 2 } + v _ { n - 1 } ^ { T } w ) ^ { - 1 } w , s _ { n } = - ( I - w _ { n - 1 } v _ { n - 1 } ^ { T } ) w. \end{equation*}
The major weakness in this formulation is the need to store two new vectors with each non-linear iteration. This can be reduced to one, [a5], [a13], at the cost of a bit more complexity. This makes Broyden's method a good algorithm for very large problems if the product $B _ { 0 } ^ { - 1 } F ( x _ { n } )$ can be evaluated efficiently.
A completely different approach, [a4], is to perform a QR-factorization (cf. Matrix factorization; Triangular matrix) of $B_0$ and update the QR-factors. This is more costly than the approach proposed above, requiring the storage of a full $( N \times N )$-matrix and an upper triangular $( N \times N )$-matrix and more floating point arithmetic. However, this dense matrix approach has better theoretical stability properties, which may be important if an extremely large number of non-linear iterations will be needed.
References
| [a1] | C.G. Broyden, "A class of methods for solving nonlinear simultaneous equations" Math. Comp. , 19 (1965) pp. 577–593 |
| [a2] | C.G. Broyden, J.E. Dennis, J.J. Moré, "On the local and superlinear convergence of quasi-Newton methods" J. Inst. Math. Appl. , 12 (1973) pp. 223–246 |
| [a3] | J.E. Dennis, J.J. Moré, "Quasi-Newton methods, methods, motivation and theory" SIAM Review , 19 (1977) pp. 46–89 |
| [a4] | J.E. Dennis, R.B. Schnabel, "Numerical Methods for Nonlinear Equations and Unconstrained Optimization" , Classics in Applied Math. : 16 , SIAM (Soc. Industrial Applied Math.) (1996) |
| [a5] | P. Deuflhard, R.W. Freund, A. Walter, "Fast Secant Methods for the Iterative Solution of Large Nonsymmetric Linear Systems" Impact of Computing in Science and Engineering , 2 (1990) pp. 244–276 |
| [a6] | M.S. Engelman, G. Strang, K.J. Bathe, "The application of quasi-Newton methods in fluid mechanics" Internat. J. Numerical Methods Eng. , 17 (1981) pp. 707–718 |
| [a7] | J.M. Ortega, W.C. Rheinboldt, "Iterative Solution of Nonlinear Equations in Several Variables" , Acad. Press (1970) |
| [a8] | J. Sherman, W.J. Morrison, "Adjustment of an inverse matrix corresponding to changes in the elements of a given column or a given row of the original matrix (abstract)" Ann. Math. Stat. , 20 (1949) pp. 621 |
| [a9] | J. Sherman, W.J. Morrison, "Adjustment of an inverse matrix corresponding to a change in one element of a given matrix" Ann. Math. Stat. , 21 (1950) pp. 124–127 |
| [a10] | D.W. Decker, H.B. Keller, C.T. Kelley, "Convergence rates for Newton's method at singular points" SIAM J. Numer. Anal. , 20 (1983) pp. 296–314 |
| [a11] | D.W. Decker, C.T. Kelley, "Sublinear convergence of the chord method at singular points" Numer. Math. , 42 (1983) pp. 147–154 |
| [a12] | D.W. Decker, C.T. Kelley, "Broyden's method for a class of problems having singular Jacobian at the root" SIAM J. Numer. Anal. , 22 (1985) pp. 566–574 |
| [a13] | C.T. Kelley, "Iterative Methods for Linear and Nonlinear Equations" , Frontiers in Appl. Math. : 16 , SIAM (Soc. Industrial Applied Math.) (1995) |
| [a14] | C.T. Kelley, E.W. Sachs, "A new proof of superlinear convergence for Broyden's method in Hilbert space" SIAM J. Optim. , 1 (1991) pp. 146–150 |
Broyden method. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Broyden_method&oldid=49912