Namespaces
Variants
Actions

Difference between revisions of "Trigonometric polynomial"

From Encyclopedia of Mathematics
Jump to: navigation, search
m (tex encoded by computer)
m (Undo revision 49036 by Ulf Rehmann (talk))
Tag: Undo
Line 1: Line 1:
−
<!--
 
−
t0942301.png
 
−
$#A+1 = 7 n = 0
 
−
$#C+1 = 7 : ~/encyclopedia/old_files/data/T094/T.0904230 Trigonometric polynomial,
 
−
Automatically converted into TeX, above some diagnostics.
 
−
Please remove this comment and the {{TEX|auto}} line below,
 
−
if TeX found to be correct.
 
−
-->
 
−
 
−
{{TEX|auto}}
 
−
{{TEX|done}}
 
−
 
 
''finite trigonometric sum''
 
''finite trigonometric sum''
  
 
An expression of the form
 
An expression of the form
  
−
$$
+
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t094/t094230/t0942301.png" /></td> </tr></table>
−
T ( x)  = {
 
−
\frac{a _ {0} }{2}
 
−
} +
 
−
\sum _ {k = 1 } ^ { n }  ( a _ {k}  \cos  kx + b _ {k}  \sin  kx)
 
−
$$
 
  
−
with real coefficients $  a _ {0} , a _ {k} , b _ {k} $,
+
with real coefficients <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t094/t094230/t0942302.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t094/t094230/t0942303.png" />; the number <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t094/t094230/t0942304.png" /> is called the order of the trigonometric polynomial (provided <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t094/t094230/t0942305.png" />). A trigonometric polynomial can be written in complex form:
−
$  k = 1 \dots n $;  
 
−
the number $  n $
 
−
is called the order of the trigonometric polynomial (provided $  | a _ {n} | + | b _ {n} | > 0 $).  
 
−
A trigonometric polynomial can be written in complex form:
 
  
−
$$
+
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t094/t094230/t0942306.png" /></td> </tr></table>
−
T ( x)  = \sum _ {k = - n } ^ { n }  c _ {k} e  ^ {ikx} ,
 
−
$$
 
  
 
where
 
where
  
−
$$
+
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t094/t094230/t0942307.png" /></td> </tr></table>
−
2c _ {k}  = \left \{
 
  
 
Trigonometric polynomials are an important tool in the [[Approximation of functions|approximation of functions]].
 
Trigonometric polynomials are an important tool in the [[Approximation of functions|approximation of functions]].
 +
 +
  
 
====Comments====
 
====Comments====
 
Cf. also [[Trigonometric series|Trigonometric series]].
 
Cf. also [[Trigonometric series|Trigonometric series]].

Revision as of 14:53, 7 June 2020

finite trigonometric sum

An expression of the form

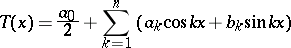with real coefficients , ; the number is called the order of the trigonometric polynomial (provided ). A trigonometric polynomial can be written in complex form:

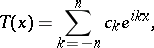where

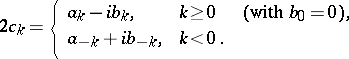Trigonometric polynomials are an important tool in the approximation of functions.


Comments

Cf. also Trigonometric series.

How to Cite This Entry:
Trigonometric polynomial. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Trigonometric_polynomial&oldid=49036
This article was adapted from an original article by V.I. Bityutskov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article
Retrieved from "https://encyclopediaofmath.org/index.php?title=Trigonometric_polynomial&oldid=49479"