Difference between revisions of "Separable process"
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
Ulf Rehmann (talk | contribs) m (Undo revision 48670 by Ulf Rehmann (talk)) Tag: Undo |
||
| Line 1: | Line 1: | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
{{MSC|60G05|60G17}} | {{MSC|60G05|60G17}} | ||
[[Category:Stochastic processes]] | [[Category:Stochastic processes]] | ||
| − | A [[Stochastic process|stochastic process]] such that the behaviour of its trajectories is essentially determined by their behaviour on a countable subset. A real stochastic process | + | A [[Stochastic process|stochastic process]] such that the behaviour of its trajectories is essentially determined by their behaviour on a countable subset. A real stochastic process <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084490/s0844901.png" /> defined on a complete probability space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084490/s0844902.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084490/s0844903.png" /> is a subset of the real line <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084490/s0844904.png" />, is separable relative to a class <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084490/s0844905.png" /> of subsets of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084490/s0844906.png" /> if there are a countable set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084490/s0844907.png" /> (the separant) and a set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084490/s0844908.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084490/s0844909.png" />, such that for any <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084490/s08449010.png" /> and for any open interval <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084490/s08449011.png" /> one has |
| − | defined on a complete probability space | ||
| − | where | ||
| − | is a subset of the real line | ||
| − | is separable relative to a class | ||
| − | of subsets of | ||
| − | if there are a countable set | ||
| − | the separant) and a set | ||
| − | |||
| − | such that for any | ||
| − | and for any open interval | ||
| − | one has | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084490/s08449012.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | Here | + | Here <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084490/s08449013.png" /> stands for the intersection <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084490/s08449014.png" />. |
| − | stands for the intersection | ||
| − | The concepts of separability relative to the class of closed sets and relative to the class of closed intervals are most important (in the latter case the process is simply called separable). If a process | + | The concepts of separability relative to the class of closed sets and relative to the class of closed intervals are most important (in the latter case the process is simply called separable). If a process <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084490/s08449015.png" /> is separable, then for any <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084490/s08449016.png" /> and any open set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084490/s08449017.png" />, |
| − | is separable, then for any | ||
| − | and any open set | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084490/s08449018.png" /></td> <td valign="top" style="width:5%;text-align:right;">(1)</td></tr></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084490/s08449019.png" /></td> <td valign="top" style="width:5%;text-align:right;">(2)</td></tr></table> | |
| − | |||
| − | |||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084490/s08449020.png" /></td> <td valign="top" style="width:5%;text-align:right;">(3)</td></tr></table> | |
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084490/s08449021.png" /></td> <td valign="top" style="width:5%;text-align:right;">(4)</td></tr></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | Each of the properties (1)–(4) is equivalent to separability. If | + | Each of the properties (1)–(4) is equivalent to separability. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084490/s08449022.png" /> is a left limit point of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084490/s08449023.png" />, then there is a sequence <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084490/s08449024.png" /> of points of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084490/s08449025.png" /> such that |
| − | is a left limit point of | ||
| − | then there is a sequence | ||
| − | of points of | ||
| − | such that | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084490/s08449026.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | with probability 1 (similarly for right limit points). If | + | with probability 1 (similarly for right limit points). If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084490/s08449027.png" /> is a separable stochastic process that is continuous in probability, then every countable everywhere-dense set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084490/s08449028.png" /> is a separant; in addition, for any open interval <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084490/s08449029.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084490/s08449030.png" />, and any sequence <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084490/s08449031.png" /> of finite subsets of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084490/s08449032.png" /> satisfying the condition <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084490/s08449033.png" />, one has |
| − | is a separable stochastic process that is continuous in probability, then every countable everywhere-dense set | ||
| − | is a separant; in addition, for any open interval | ||
| − | |||
| − | and any sequence | ||
| − | of finite subsets of | ||
| − | satisfying the condition | ||
| − | one has | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084490/s08449034.png" /></td> <td valign="top" style="width:5%;text-align:right;">(5)</td></tr></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | in probability. The convergence in (5) can be replaced by convergence with probability 1 if | + | in probability. The convergence in (5) can be replaced by convergence with probability 1 if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084490/s08449035.png" /> is continuous with probability 1. |
| − | is continuous with probability 1. | ||
| − | For any stochastic process | + | For any stochastic process <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084490/s08449036.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084490/s08449037.png" />, there is a process <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084490/s08449038.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084490/s08449039.png" />, on the same probability space that is separable relative to the class of closed sets, takes values in the extended real line and is such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084490/s08449040.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084490/s08449041.png" />. The concept of separability and its properties can be generalized to processes for which <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084490/s08449042.png" /> and the range of values are different general topological spaces. The transition to a separable process enables one to assert the measurability of a number of important functionals and sets connected with a process. An alternative approach consists in extending the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084490/s08449043.png" />-algebra on which it is defined (for example, in the case of a product of Hausdorff compacta, a measure can be uniquely extended from the usual <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084490/s08449044.png" />-algebra generated by cylindrical sets to the very rich <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084490/s08449045.png" />-algebra of Borel sets), rather than in replacing the random variables constituting the process. |
| − | |||
| − | there is a process | ||
| − | |||
| − | on the same probability space that is separable relative to the class of closed sets, takes values in the extended real line and is such that | ||
| − | |||
| − | The concept of separability and its properties can be generalized to processes for which | ||
| − | and the range of values are different general topological spaces. The transition to a separable process enables one to assert the measurability of a number of important functionals and sets connected with a process. An alternative approach consists in extending the | ||
| − | algebra on which it is defined (for example, in the case of a product of Hausdorff compacta, a measure can be uniquely extended from the usual | ||
| − | algebra generated by cylindrical sets to the very rich | ||
| − | algebra of Borel sets), rather than in replacing the random variables constituting the process. | ||
====References==== | ====References==== | ||
Revision as of 14:53, 7 June 2020
2020 Mathematics Subject Classification: Primary: 60G05 Secondary: 60G17 [MSN][ZBL]
A stochastic process such that the behaviour of its trajectories is essentially determined by their behaviour on a countable subset. A real stochastic process  defined on a complete probability space
defined on a complete probability space 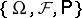 , where
, where 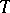 is a subset of the real line
is a subset of the real line  , is separable relative to a class
, is separable relative to a class  of subsets of
of subsets of  if there are a countable set
if there are a countable set 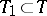 (the separant) and a set
(the separant) and a set 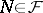 ,
, 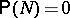 , such that for any
, such that for any 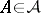 and for any open interval
and for any open interval 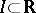 one has
one has
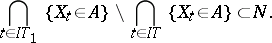 |
Here 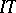 stands for the intersection
stands for the intersection 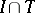 .
.
The concepts of separability relative to the class of closed sets and relative to the class of closed intervals are most important (in the latter case the process is simply called separable). If a process 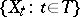 is separable, then for any
is separable, then for any 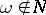 and any open set
and any open set 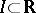 ,
,
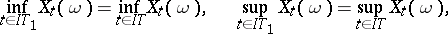 | (1) |
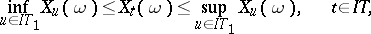 | (2) |
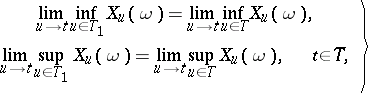 | (3) |
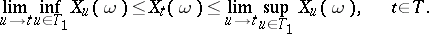 | (4) |
Each of the properties (1)–(4) is equivalent to separability. If 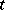 is a left limit point of
is a left limit point of 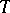 , then there is a sequence
, then there is a sequence 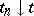 of points of
of points of 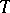 such that
such that
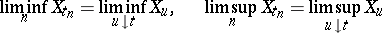 |
with probability 1 (similarly for right limit points). If 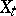 is a separable stochastic process that is continuous in probability, then every countable everywhere-dense set
is a separable stochastic process that is continuous in probability, then every countable everywhere-dense set 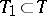 is a separant; in addition, for any open interval
is a separant; in addition, for any open interval 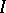 ,
, 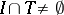 , and any sequence
, and any sequence 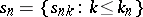 of finite subsets of
of finite subsets of  satisfying the condition
satisfying the condition 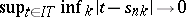 , one has
, one has
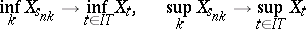 | (5) |
in probability. The convergence in (5) can be replaced by convergence with probability 1 if 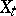 is continuous with probability 1.
is continuous with probability 1.
For any stochastic process 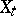 ,
,  , there is a process
, there is a process 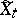 ,
, 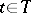 , on the same probability space that is separable relative to the class of closed sets, takes values in the extended real line and is such that
, on the same probability space that is separable relative to the class of closed sets, takes values in the extended real line and is such that  ,
, 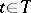 . The concept of separability and its properties can be generalized to processes for which
. The concept of separability and its properties can be generalized to processes for which 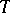 and the range of values are different general topological spaces. The transition to a separable process enables one to assert the measurability of a number of important functionals and sets connected with a process. An alternative approach consists in extending the
and the range of values are different general topological spaces. The transition to a separable process enables one to assert the measurability of a number of important functionals and sets connected with a process. An alternative approach consists in extending the 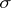 -algebra on which it is defined (for example, in the case of a product of Hausdorff compacta, a measure can be uniquely extended from the usual
-algebra on which it is defined (for example, in the case of a product of Hausdorff compacta, a measure can be uniquely extended from the usual  -algebra generated by cylindrical sets to the very rich
-algebra generated by cylindrical sets to the very rich 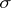 -algebra of Borel sets), rather than in replacing the random variables constituting the process.
-algebra of Borel sets), rather than in replacing the random variables constituting the process.
References
| [D] | J.L. Doob, "Stochastic processes" , Chapman & Hall (1953) MR1570654 MR0058896 Zbl 0053.26802 |
| [L] | M. Loève, "Probability theory" , Princeton Univ. Press (1963) MR0203748 Zbl 0108.14202 |
| [GS] | I.I. Gihman, A.V. Skorohod, "The theory of stochastic processes" , 1 , Springer (1971) (Translated from Russian) MR0636254 MR0651015 MR0375463 MR0346882 Zbl 0531.60002 Zbl 0531.60001 Zbl 0404.60061 Zbl 0305.60027 Zbl 0291.60019 |
| [D2] | J.L. Doob, "Probability in function space" Bull. Amer. Math. Soc. , 53 : 1 (1947) pp. 15–30 MR0019858 Zbl 0032.03401 |
| [N] | E. Nelson, "Regular probability measures on function space" Ann. of Math. , 69 : 3 (1959) pp. 630–643 MR0105743 Zbl 0087.13102 |
Separable process. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Separable_process&oldid=48670