Difference between revisions of "Riemann differential equation"
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
Ulf Rehmann (talk | contribs) m (Undo revision 48545 by Ulf Rehmann (talk)) Tag: Undo |
||
| Line 1: | Line 1: | ||
| − | < | + | A linear homogeneous ordinary differential equation of the second order in the complex plane with three given regular singular points (cf. [[Regular singular point|Regular singular point]]) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081870/r0818701.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081870/r0818702.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081870/r0818703.png" /> having characteristic exponents <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081870/r0818704.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081870/r0818705.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081870/r0818706.png" /> at these points. The general form of such an equation was first given by E. Papperitz, because of which it is also known as a [[Papperitz equation|Papperitz equation]]. Solutions of a Riemann differential equation are written in the form of the so-called Riemann <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081870/r0818708.png" />-function |
| − | r0818701.png | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081870/r0818709.png" /></td> </tr></table> | |
| − | |||
| − | + | Riemann differential equations belong to the class of Fuchsian equations (cf. [[Fuchsian equation|Fuchsian equation]]) with three singular points. A particular case of Riemann differential equations is the [[Hypergeometric equation|hypergeometric equation]] (the singular points are <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r081/r081870/r08187010.png" />); therefore, a Riemann differential equation itself is sometimes known as a generalized hypergeometric equation. A Riemann differential equation can be reduced to a [[Pochhammer equation|Pochhammer equation]], and its solution can thus be written in the form of an integral over a special contour in the complex plane. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | Riemann differential equations belong to the class of Fuchsian equations (cf. [[Fuchsian equation|Fuchsian equation]]) with three singular points. A particular case of Riemann differential equations is the [[Hypergeometric equation|hypergeometric equation]] (the singular points are | ||
| − | therefore, a Riemann differential equation itself is sometimes known as a generalized hypergeometric equation. A Riemann differential equation can be reduced to a [[Pochhammer equation|Pochhammer equation]], and its solution can thus be written in the form of an integral over a special contour in the complex plane. | ||
For references see [[Papperitz equation|Papperitz equation]]. | For references see [[Papperitz equation|Papperitz equation]]. | ||
Revision as of 14:53, 7 June 2020
A linear homogeneous ordinary differential equation of the second order in the complex plane with three given regular singular points (cf. Regular singular point)  ,
,  and
and  having characteristic exponents
having characteristic exponents  ,
,  ,
,  at these points. The general form of such an equation was first given by E. Papperitz, because of which it is also known as a Papperitz equation. Solutions of a Riemann differential equation are written in the form of the so-called Riemann
at these points. The general form of such an equation was first given by E. Papperitz, because of which it is also known as a Papperitz equation. Solutions of a Riemann differential equation are written in the form of the so-called Riemann  -function
-function
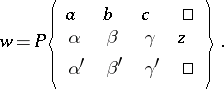 |
Riemann differential equations belong to the class of Fuchsian equations (cf. Fuchsian equation) with three singular points. A particular case of Riemann differential equations is the hypergeometric equation (the singular points are 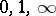 ); therefore, a Riemann differential equation itself is sometimes known as a generalized hypergeometric equation. A Riemann differential equation can be reduced to a Pochhammer equation, and its solution can thus be written in the form of an integral over a special contour in the complex plane.
); therefore, a Riemann differential equation itself is sometimes known as a generalized hypergeometric equation. A Riemann differential equation can be reduced to a Pochhammer equation, and its solution can thus be written in the form of an integral over a special contour in the complex plane.
For references see Papperitz equation.
Riemann differential equation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Riemann_differential_equation&oldid=48545