Difference between revisions of "Regulator of an algebraic number field"
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
Ulf Rehmann (talk | contribs) m (Undo revision 48493 by Ulf Rehmann (talk)) Tag: Undo |
||
| Line 1: | Line 1: | ||
| − | < | + | ''<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080950/r0809501.png" />'' |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | The number <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080950/r0809502.png" /> that is, by definition, equal to 1 if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080950/r0809503.png" /> is the field <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080950/r0809504.png" /> or an imaginary quadratic extension of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080950/r0809505.png" />, and to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080950/r0809506.png" /> in all other cases, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080950/r0809507.png" /> is the rank of the group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080950/r0809508.png" /> of units of the field <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080950/r0809509.png" /> (see [[Algebraic number|Algebraic number]]; [[Algebraic number theory|Algebraic number theory]]) and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080950/r08095010.png" /> is the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080950/r08095011.png" />-dimensional volume of the basic parallelepipedon of the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080950/r08095012.png" />-dimensional lattice in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080950/r08095013.png" /> that is the image of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080950/r08095014.png" /> under its logarithmic mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080950/r08095015.png" /> into <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080950/r08095016.png" />. The homomorphism <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080950/r08095017.png" /> is defined as follows: Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080950/r08095018.png" /> be all real and let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080950/r08095019.png" /> be all pairwise complex non-conjugate isomorphisms of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080950/r08095020.png" /> into <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080950/r08095021.png" />; <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080950/r08095022.png" />. Then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080950/r08095023.png" /> (see [[Dirichlet theorem|Dirichlet theorem]] on units), and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080950/r08095024.png" /> is defined by the formula | |
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080950/r08095025.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
where | where | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080950/r08095026.png" /></td> </tr></table> | |
| − | |||
| − | The image of | + | The image of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080950/r08095027.png" /> under <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080950/r08095028.png" /> is an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080950/r08095029.png" />-dimensional lattice in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080950/r08095030.png" /> lying in the plane <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080950/r08095031.png" /> (where the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080950/r08095032.png" /> are the canonical coordinates). |
| − | under | ||
| − | is an | ||
| − | dimensional lattice in | ||
| − | lying in the plane | ||
| − | where the | ||
| − | are the canonical coordinates). | ||
| − | Units | + | Units <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080950/r08095033.png" /> for which <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080950/r08095034.png" /> form a basis of the lattice <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080950/r08095035.png" /> are known as fundamental units of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080950/r08095036.png" />, and |
| − | for which | ||
| − | form a basis of the lattice | ||
| − | are known as fundamental units of | ||
| − | and | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080950/r08095037.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | There are other formulas linking the regulator with other invariants of the field | + | There are other formulas linking the regulator with other invariants of the field <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080950/r08095038.png" /> (see, for example, [[Discriminant|Discriminant]], 3). |
| − | see, for example, [[Discriminant|Discriminant]], 3). | ||
| − | If instead of | + | If instead of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080950/r08095039.png" /> one considers the intersection of this group with an order <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080950/r08095040.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080950/r08095041.png" />, then the regulator <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080950/r08095042.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080950/r08095043.png" /> can be defined in the same way. |
| − | one considers the intersection of this group with an order | ||
| − | of | ||
| − | then the regulator | ||
| − | of | ||
| − | can be defined in the same way. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> Z.I. Borevich, I.R. Shafarevich, "Number theory" , Acad. Press (1987) (Translated from Russian) (German translation: Birkhäuser, 1966)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> S. Lang, "Algebraic number theory" , Addison-Wesley (1970)</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> Z.I. Borevich, I.R. Shafarevich, "Number theory" , Acad. Press (1987) (Translated from Russian) (German translation: Birkhäuser, 1966)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> S. Lang, "Algebraic number theory" , Addison-Wesley (1970)</TD></TR></table> | ||
Revision as of 14:53, 7 June 2020

The number  that is, by definition, equal to 1 if
that is, by definition, equal to 1 if  is the field
is the field  or an imaginary quadratic extension of
or an imaginary quadratic extension of  , and to
, and to  in all other cases, where
in all other cases, where  is the rank of the group
is the rank of the group  of units of the field
of units of the field  (see Algebraic number; Algebraic number theory) and
(see Algebraic number; Algebraic number theory) and  is the
is the  -dimensional volume of the basic parallelepipedon of the
-dimensional volume of the basic parallelepipedon of the  -dimensional lattice in
-dimensional lattice in 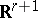 that is the image of
that is the image of  under its logarithmic mapping
under its logarithmic mapping 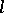 into
into 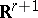 . The homomorphism
. The homomorphism  is defined as follows: Let
is defined as follows: Let  be all real and let
be all real and let  be all pairwise complex non-conjugate isomorphisms of
be all pairwise complex non-conjugate isomorphisms of 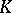 into
into  ;
; 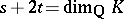 . Then
. Then  (see Dirichlet theorem on units), and
(see Dirichlet theorem on units), and 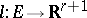 is defined by the formula
is defined by the formula
 |
where
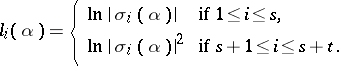 |
The image of 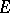 under
under 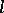 is an
is an  -dimensional lattice in
-dimensional lattice in 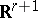 lying in the plane
lying in the plane  (where the
(where the 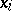 are the canonical coordinates).
are the canonical coordinates).
Units  for which
for which 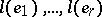 form a basis of the lattice
form a basis of the lattice 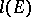 are known as fundamental units of
are known as fundamental units of  , and
, and
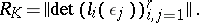 |
There are other formulas linking the regulator with other invariants of the field  (see, for example, Discriminant, 3).
(see, for example, Discriminant, 3).
If instead of  one considers the intersection of this group with an order
one considers the intersection of this group with an order 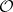 of
of 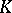 , then the regulator
, then the regulator 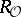 of
of 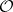 can be defined in the same way.
can be defined in the same way.
References
| [1] | Z.I. Borevich, I.R. Shafarevich, "Number theory" , Acad. Press (1987) (Translated from Russian) (German translation: Birkhäuser, 1966) |
| [2] | S. Lang, "Algebraic number theory" , Addison-Wesley (1970) |
Regulator of an algebraic number field. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Regulator_of_an_algebraic_number_field&oldid=48493