Difference between revisions of "Anti-Lie triple system"
m (link) |
m (link) |
||
| Line 1: | Line 1: | ||
| − | A triple system is a [[Vector space|vector space]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a130/a130250/a1302501.png" /> over a field <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a130/a130250/a1302502.png" /> together with a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a130/a130250/a1302503.png" />-[[trilinear mapping]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a130/a130250/a1302504.png" />. A triple system <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a130/a130250/a1302505.png" /> satisfying | + | A [[triple system]] is a [[Vector space|vector space]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a130/a130250/a1302501.png" /> over a field <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a130/a130250/a1302502.png" /> together with a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a130/a130250/a1302503.png" />-[[trilinear mapping]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a130/a130250/a1302504.png" />. A triple system <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a130/a130250/a1302505.png" /> satisfying |
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a130/a130250/a1302506.png" /></td> <td valign="top" style="width:5%;text-align:right;">(a1)</td></tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a130/a130250/a1302506.png" /></td> <td valign="top" style="width:5%;text-align:right;">(a1)</td></tr></table> | ||
Revision as of 18:11, 19 March 2018
A triple system is a vector space 
over a field 
together with a 
-trilinear mapping 
. A triple system 
satisfying
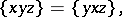 | (a1) |
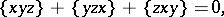 | (a2) |
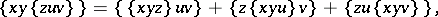 | (a3) |
for all 
, is called an anti-Lie triple system.
If instead of (a1) one has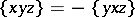 
, a Lie triple system is obtained.
Assume that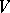 
is an anti-Lie triple system and that 
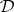is the Lie algebra of derivations of 
containing the inner derivation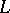 
defined by 
. Consider 
with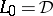 
and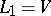 
, and with product given by 
, 
, 
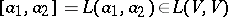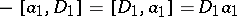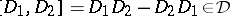for 
, 
(
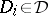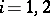). Then the definition of anti-Lie triple system implies that 
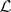is a Lie superalgebra (cf. also Lie algebra). Hence 
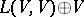is an ideal of the Lie superalgebra 
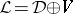. One denotes 
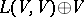by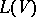 
and calls it the standard embedding Lie superalgebra of 
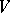. This concept is useful to obtain a construction of Lie superalgebras as well as a construction of Lie algebras from Lie triple systems.
References
| [a1] | J.R. Faulkner, J.C. Ferrar, "Simple anti-Jordan pairs" Commun. Algebra , 8 (1980) pp. 993–1013 |
| [a2] | N. Kamiya, "A construction of anti-Lie triple systems from a class of triple systems" Memoirs Fac. Sci. Shimane Univ. , 22 (1988) pp. 51–62 |
Anti-Lie triple system. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Anti-Lie_triple_system&oldid=41898