Difference between revisions of "Lie triple system"
m (link) |
m (link) |
||
| Line 21: | Line 21: | ||
This algebra is called the standard embedding Lie algebra associated with the Lie triple system <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l130/l130040/l13004024.png" />. This implies that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l130/l130040/l13004025.png" /> is a homogeneous symmetric space (cf. also [[Homogeneous space|Homogeneous space]]; [[Symmetric space|Symmetric space]]), that is, it is important in the correspondence with geometric phenomena and algebraic systems. The relationship between Riemannian globally symmetric spaces and Lie triple systems is given in [[#References|[a4]]], and the relationship between totally geodesic submanifolds and Lie triple systems is given in [[#References|[a1]]]. A general consideration of supertriple systems is given in [[#References|[a2]]] and [[#References|[a5]]]. | This algebra is called the standard embedding Lie algebra associated with the Lie triple system <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l130/l130040/l13004024.png" />. This implies that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l130/l130040/l13004025.png" /> is a homogeneous symmetric space (cf. also [[Homogeneous space|Homogeneous space]]; [[Symmetric space|Symmetric space]]), that is, it is important in the correspondence with geometric phenomena and algebraic systems. The relationship between Riemannian globally symmetric spaces and Lie triple systems is given in [[#References|[a4]]], and the relationship between totally geodesic submanifolds and Lie triple systems is given in [[#References|[a1]]]. A general consideration of supertriple systems is given in [[#References|[a2]]] and [[#References|[a5]]]. | ||
| − | Note that this kind of triple system is completely different from the combinatorial one of, e.g., a | + | Note that this kind of triple system is completely different from the combinatorial one of, e.g., a [[Steiner triple system]]. |
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> S. Helgason, "Differential geometry, Lie groups, and symmetric spaces" , Acad. Press (1978)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> N. Kamiya, S. Okubo, "On <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l130/l130040/l13004026.png" />-Lie supertriple systems associated with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l130/l130040/l13004027.png" />-Freudenthal–Kantor supertriple systems" ''Proc. Edinburgh Math. Soc.'' , '''43''' (2000) pp. 243–260</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> W.G. Lister, "A structure theory of Lie triple systems" ''Trans. Amer. Math. Soc.'' , '''72''' (1952) pp. 217–242</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> O. Loos, "Symmetric spaces" , Benjamin (1969)</TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> S. Okubo, N. Kamiya, "Jordan–Lie super algebra and Jordan–Lie triple system" ''J. Algebra'' , '''198''' : 2 (1997) pp. 388–411</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> S. Helgason, "Differential geometry, Lie groups, and symmetric spaces" , Acad. Press (1978)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> N. Kamiya, S. Okubo, "On <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l130/l130040/l13004026.png" />-Lie supertriple systems associated with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l130/l130040/l13004027.png" />-Freudenthal–Kantor supertriple systems" ''Proc. Edinburgh Math. Soc.'' , '''43''' (2000) pp. 243–260</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> W.G. Lister, "A structure theory of Lie triple systems" ''Trans. Amer. Math. Soc.'' , '''72''' (1952) pp. 217–242</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> O. Loos, "Symmetric spaces" , Benjamin (1969)</TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> S. Okubo, N. Kamiya, "Jordan–Lie super algebra and Jordan–Lie triple system" ''J. Algebra'' , '''198''' : 2 (1997) pp. 388–411</TD></TR></table> | ||
Revision as of 15:13, 19 March 2018
A triple system is a vector space  over a field
over a field  together with a
together with a  -trilinear mapping
-trilinear mapping 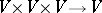 .
.
A vector space  with triple product
with triple product  is said to be a Lie triple system if
is said to be a Lie triple system if
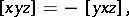 | (a1) |
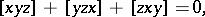 | (a2) |
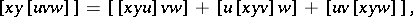 | (a3) |
for all  .
.
Setting 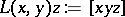 , then (a3) means that the left endomorphism
, then (a3) means that the left endomorphism 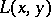 is a derivation of
is a derivation of 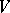 (cf. also Derivation in a ring). Thus one denotes
(cf. also Derivation in a ring). Thus one denotes 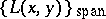 by
by 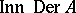 .
.
Let 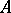 be a Lie triple system and let
be a Lie triple system and let 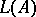 be the vector space of the direct sum of
be the vector space of the direct sum of 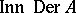 and
and  . Then
. Then 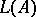 is a Lie algebra with respect to the product
is a Lie algebra with respect to the product
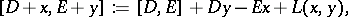 |
where 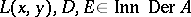 ,
,  .
.
This algebra is called the standard embedding Lie algebra associated with the Lie triple system 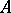 . This implies that
. This implies that 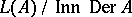 is a homogeneous symmetric space (cf. also Homogeneous space; Symmetric space), that is, it is important in the correspondence with geometric phenomena and algebraic systems. The relationship between Riemannian globally symmetric spaces and Lie triple systems is given in [a4], and the relationship between totally geodesic submanifolds and Lie triple systems is given in [a1]. A general consideration of supertriple systems is given in [a2] and [a5].
is a homogeneous symmetric space (cf. also Homogeneous space; Symmetric space), that is, it is important in the correspondence with geometric phenomena and algebraic systems. The relationship between Riemannian globally symmetric spaces and Lie triple systems is given in [a4], and the relationship between totally geodesic submanifolds and Lie triple systems is given in [a1]. A general consideration of supertriple systems is given in [a2] and [a5].
Note that this kind of triple system is completely different from the combinatorial one of, e.g., a Steiner triple system.
References
| [a1] | S. Helgason, "Differential geometry, Lie groups, and symmetric spaces" , Acad. Press (1978) |
| [a2] | N. Kamiya, S. Okubo, "On 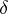 -Lie supertriple systems associated with -Lie supertriple systems associated with 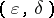 -Freudenthal–Kantor supertriple systems" Proc. Edinburgh Math. Soc. , 43 (2000) pp. 243–260 -Freudenthal–Kantor supertriple systems" Proc. Edinburgh Math. Soc. , 43 (2000) pp. 243–260 |
| [a3] | W.G. Lister, "A structure theory of Lie triple systems" Trans. Amer. Math. Soc. , 72 (1952) pp. 217–242 |
| [a4] | O. Loos, "Symmetric spaces" , Benjamin (1969) |
| [a5] | S. Okubo, N. Kamiya, "Jordan–Lie super algebra and Jordan–Lie triple system" J. Algebra , 198 : 2 (1997) pp. 388–411 |
Lie triple system. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Lie_triple_system&oldid=41897