Difference between revisions of "Co-algebra"
(TeX partly done) |
(TeX partly done) |
||
| Line 19: | Line 19: | ||
====Comments==== | ====Comments==== | ||
| − | Given a co-algebra $A$ over $k$, let $A^*$ be the module of $k$-module homomorphisms from $A$ to $k$. For $f,g \in A^*$ define the product $fg : A \to k$ by the formula $fg : a \mapsto (f\otimes g)(\phi(a))$, where $k \otimes_k k$ is identified with $k$. For any two $k$-modules $M,N$ define $\rho : M^* \otimes N^* \to (M \otimes N)^*$ by $\rho(f\otimes g)(m\otimes n) = f(m)g(n)$. Then the multiplication on | + | Given a co-algebra $A$ over $k$, let $A^*$ be the module of $k$-module homomorphisms from $A$ to $k$. For $f,g \in A^*$ define the product $fg : A \to k$ by the formula $fg : a \mapsto (f\otimes g)(\phi(a))$, where $k \otimes_k k$ is identified with $k$. For any two $k$-modules $M,N$ define $\rho : M^* \otimes N^* \to (M \otimes N)^*$ by $\rho(f\otimes g)(m\otimes n) = f(m)g(n)$. Then the multiplication on $A^*$ can also be seen as the composite $A^* \otimes A^* \to (A\otimes A)^* \stackrel{\phi^*}{\to} A^*$. The element $\epsilon : A \to k$ is a unit element for this multiplication making $A^*$ an associative algebra with unit, the dual algebra. In general the mapping $\rho$ is not an isomorphism and there is no natural $k$-module homomorphism $M^* \otimes N^* \to (M \otimes N)^*$. Thus there is no equally natural construction associating a co-algebra to an algebra over $k$, even when $k$ is a field. In that case there does however exist an [[adjoint functor]] $A \mapsto A^0$ to the functor $C \to C^*$ which associates to a co-algebra its dual algebra, i.e. <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022670/c02267034.png" /> for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022670/c02267035.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022670/c02267036.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022670/c02267037.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022670/c02267038.png" /> denote, respectively, the category of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022670/c02267039.png" />-algebras and the category of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022670/c02267040.png" />-co-algebras, [[#References|[a2]]]; cf. also [[Hopf algebra|Hopf algebra]]. But if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022670/c02267041.png" /> is free of finite rank over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022670/c02267042.png" /> then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022670/c02267043.png" /> is an isomorphism and the dual co-algebra can be defined. |
Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022670/c02267044.png" /> be the set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022670/c02267045.png" />. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022670/c02267046.png" /> and define | Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022670/c02267044.png" /> be the set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022670/c02267045.png" />. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022670/c02267046.png" /> and define | ||
Revision as of 21:09, 10 April 2017
A module $A$ over a commutative ring $k$ with two homomorphisms $\phi$ and $\epsilon$ such that the diagrams
$$
\begin{array}{ccc} A & \stackrel{\phi}{\rightarrow} & A \otimes A \\ \phi\,\downarrow & \ & \downarrow\,1 \otimes \phi \\ A \otimes A & \stackrel{\phi \otimes 1}{\longrightarrow} & A \otimes A \end{array}
$$
and
$$
\begin{array}{ccccc} A \otimes A & \stackrel{\phi}{\leftarrow} & A & \stackrel{\phi}{\rightarrow} & A \otimes A \\ & \searrow\,\epsilon\otimes1\ & & 1\otimes\epsilon\,\swarrow & \\ & & A & & \end{array}
$$
are commutative. In other words, a co-algebra is the dual concept (in the sense of category theory) to the concept of an associative algebra over a ring 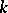 .
.
Co-algebras have acquired significance in connection with a number of topological applications such as, for example, the simplicial complex of a topological space, which is a co-algebra. Closely related to co-algebras are the Hopf algebras, which possess algebra and co-algebra structures simultaneously (cf. Hopf algebra).
References
| [1] | S. MacLane, "Homology" , Springer (1963) |
Comments
Given a co-algebra $A$ over $k$, let $A^*$ be the module of $k$-module homomorphisms from $A$ to $k$. For $f,g \in A^*$ define the product $fg : A \to k$ by the formula $fg : a \mapsto (f\otimes g)(\phi(a))$, where $k \otimes_k k$ is identified with $k$. For any two $k$-modules $M,N$ define $\rho : M^* \otimes N^* \to (M \otimes N)^*$ by $\rho(f\otimes g)(m\otimes n) = f(m)g(n)$. Then the multiplication on $A^*$ can also be seen as the composite $A^* \otimes A^* \to (A\otimes A)^* \stackrel{\phi^*}{\to} A^*$. The element $\epsilon : A \to k$ is a unit element for this multiplication making $A^*$ an associative algebra with unit, the dual algebra. In general the mapping $\rho$ is not an isomorphism and there is no natural $k$-module homomorphism $M^* \otimes N^* \to (M \otimes N)^*$. Thus there is no equally natural construction associating a co-algebra to an algebra over $k$, even when $k$ is a field. In that case there does however exist an adjoint functor $A \mapsto A^0$ to the functor $C \to C^*$ which associates to a co-algebra its dual algebra, i.e. 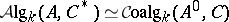 for
for 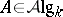 ,
, 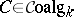 , where
, where 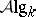 and
and 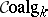 denote, respectively, the category of
denote, respectively, the category of 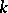 -algebras and the category of
-algebras and the category of 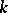 -co-algebras, [a2]; cf. also Hopf algebra. But if
-co-algebras, [a2]; cf. also Hopf algebra. But if 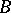 is free of finite rank over
is free of finite rank over 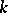 then
then 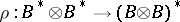 is an isomorphism and the dual co-algebra can be defined.
is an isomorphism and the dual co-algebra can be defined.
Let 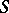 be the set
be the set 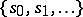 . Let
. Let 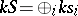 and define
and define
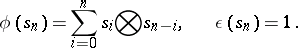 |
Then 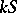 is a co-algebra.
is a co-algebra.
If 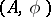 and
and 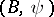 are two co-algebras, then a morphism of co-algebras is a
are two co-algebras, then a morphism of co-algebras is a 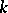 -module morphism
-module morphism 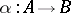 such that
such that 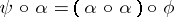 and
and 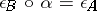 . A co-ideal of a co-algebra
. A co-ideal of a co-algebra 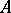 is a
is a 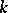 -submodule
-submodule 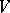 such that
such that 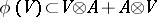 and
and 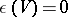 .
.
A co-module 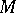 over a co-algebra
over a co-algebra 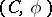 is a
is a 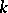 -module with a
-module with a 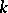 -module morphism
-module morphism 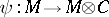 such that
such that 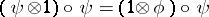 and
and 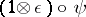 the canonical isomorphism
the canonical isomorphism 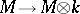 . There are obvious notions of homomorphisms of co-modules, etc.
. There are obvious notions of homomorphisms of co-modules, etc.
References
| [a1] | M. Sweedler, "Hopf algebras" , Benjamin (1969) |
| [a2] | E. Abe, "Hopf algebras" , Cambridge Univ. Press (1980) |
Co-algebra. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Co-algebra&oldid=40932