Difference between revisions of "Idempotent semi-ring"
(TeX partly done) |
(→Example 1.: TeX) |
||
| Line 22: | Line 22: | ||
===Example 1.=== | ===Example 1.=== | ||
| − | Let | + | Let $\mathbf{R}_{\max}$ be the set $A = \mathbf{R} \cup \{-\infty\}$ (where $\mathbf{R}$ is the field of real numbers) equipped with the operations $\oplus = {\max}$ and $\odot = {+}$ (usual addition); set $\mathbf{0} = -\infty$, $\mathbf{1} = 0$. Similarly, let $\mathbf{R}_{\min}$ be the set $\mathbf {R} \cup \{+\infty\}$ equipped with the operations $\oplus = {\min}$ and $\odot = {+}$; in this case $\mathbf{0} = +\infty$ and $\mathbf{1} = 0$. It is easy to check that $\mathbf{R}_{\max}$ and $\mathbf{R}_{\min}$ are (isomorphic) commutative idempotent semi-rings. |
===Example 2.=== | ===Example 2.=== | ||
Revision as of 16:07, 4 June 2016
dioid
A semi-ring with idempotent addition. So, a set $A$ equipped with binary operations $\oplus$ (addition) and $\odot$ (multiplication) and neutral elements $0$ and $1$ is called an idempotent semi-ring if the following basic properties are valid for all elements $a,b,c \in A$:
i) $a \oplus a = a$ (idempotent addition);
ii) $a \oplus (b \oplus c) = (a \oplus b) \oplus c$;
iii) $a \oplus b = b \oplus a$;
iv) $0 \oplus a = a \oplus 0 = a$;
v) $0 \odot a = a \odot 0 = 0$;
vi) $1 \odot a = a \odot 1 = a$;
vii) $a \odot (c \oplus c) = (a \odot b) \oplus (a \odot c)$;
viii) $(b \oplus c) \odot a = (b \odot a) \oplus (c \odot a)$.
An idempotent semi-ring $A$ is commutative if $a \odot b = b \odot a$ for all $a,b \in A$. Different versions of this axiomatics are used, see e.g. [a1], [a2], [a3], [a4], [a5], [a6], [a7], [a8], [a9], [a10]. Idempotent semi-rings are often called dioids, see e.g. [a3], [a9]. The concept of an idempotent semi-ring is a basic concept in idempotent analysis. This concept has many applications in different optimization problems (including dynamic programming), computer science, automata and formal language theory, numerical methods, parallel programming, etc. (cf. also Idempotent algorithm and [a1], [a2], [a3], [a4], [a5], [a6], [a7], [a8], [a9], [a10], [a11]).
Example 1.
Let $\mathbf{R}_{\max}$ be the set $A = \mathbf{R} \cup \{-\infty\}$ (where $\mathbf{R}$ is the field of real numbers) equipped with the operations $\oplus = {\max}$ and $\odot = {+}$ (usual addition); set $\mathbf{0} = -\infty$, $\mathbf{1} = 0$. Similarly, let $\mathbf{R}_{\min}$ be the set $\mathbf {R} \cup \{+\infty\}$ equipped with the operations $\oplus = {\min}$ and $\odot = {+}$; in this case $\mathbf{0} = +\infty$ and $\mathbf{1} = 0$. It is easy to check that $\mathbf{R}_{\max}$ and $\mathbf{R}_{\min}$ are (isomorphic) commutative idempotent semi-rings.
Example 2.
Let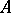 
be the set 
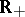of all non-negative real numbers endowed with the operations 
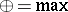and 
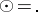(usual multiplication); 
, 
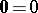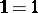. This idempotent semi-ring is isomorphic to 
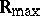. The isomorphism is given by 
.
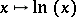Example 3.
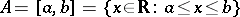with the operations 
, 
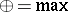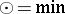and neutral elements 
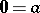and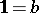 
(the cases 
, 
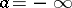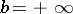are possible).
Example 4.
Let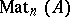 
be the set of 
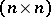-matrices with entries belonging to an idempotent semi-ring 
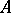. Then 
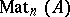is a non-commutative idempotent semi-ring with respect to matrix addition and matrix multiplication.
The Boolean algebra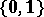 
is an example of a finite idempotent semi-ring. There are many other interesting examples of idempotent semi-rings, see e.g. [a1], [a2], [a3], [a4], [a5], [a6], [a7], [a8], [a9], [a10], [a11].
There is a natural partial order on any idempotent semi-ring (as well as on any idempotent semi-group; cf. also Idempotent semi-ring). By definition,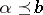 
if and only if 
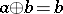. For this relation, reflexivity is equivalent to idempotency of the (generalized) addition, whereas transitivity, respectively anti-symmetry, follow from associativity, respectively commutativity, of this operation. On 
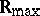(and also on the semi-rings described in the Examples 2 and 3), this ordering relation coincides with the natural one; on 
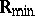it is the opposite of the natural ordering relation on the real axis. Every element 
in an idempotent semi-ring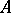 
is "non-negative" : 
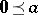. Indeed, 
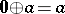. Similarly, for all 
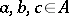one has 
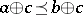, and 
if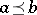 
. Using this standard partial order it is possible to define in the usual way the notions of upper and lower bounds, bounded sets, 
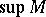(and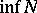 
) for upper- (lower-) bounded sets 
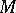(respectively, 
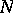), etc.
If the multiplication in a semi-ring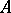 
is invertible on 
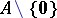, then 
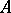is called a semi-field. For example, 
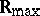is a semi-field. Idempotent semi-fields and semi-rings with idempotent multiplication are especially interesting.
References
| [a1] | A.V. Aho, J.E. Hopcroft, J.D. Ullman, "The design and analysis of computer algorithms" , Addison-Wesley (1976) |
| [a2] | B.A. Carré, "Graphs and networks" , Clarendon Press and Oxford Univ. Press (1979) |
| [a3] | M. Gondran, M. Minoux, "Graphes et algorithms" , Ed. Eyrolles (1979; 1988) |
| [a4] | R.A. Cuningham-Green, "Minimax algebra" , Lecture Notes in Economics and Mathematical Systems , 166 , Springer (1979) |
| [a5] | U. Zimmermann, "Linear and combinatorial optimization in ordered algebraic structures" Ann. Discrete Math. , 10 (1981) pp. 1–380 |
| [a6] | "Mathematical aspects of computer engineering" V.P. Maslov (ed.) K.A. Volosov (ed.) , MIR (1988) (In Russian) |
| [a7] | "Idempotent analysis" V.P. Maslov (ed.) S.N. Samborskii (ed.) , Amer. Math. Soc. (1992) (In Russian) |
| [a8] | V.N. Kolokoltsov, V.P. Maslov, "Idempotent analysis and applications" , Kluwer Acad. Publ. (1996) (In Russian) |
| [a9] | F.L. Baccelli, G. Cohen, G.J. Olsder, J.-P. Quadrat, "Synchronization and linearity: an algebra for discrete event systems" , Wiley (1992) |
| [a10] | J.S. Golan, "The theory of semirings with applications in mathematics and theoretical computer science" , Pitman monographs and surveys in pure and applied mathematics , 54 , Longman (1992) |
| [a11] | "Idempotency" J. Gunawardena (ed.) , Publ. Isaac Newton Institute 11, Cambridge Univ. Press (1998) ISBN 0-521-55344-X Zbl 0882.00035 |
Idempotent semi-ring. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Idempotent_semi-ring&oldid=38925