Difference between revisions of "Algebraic logic"
m (AUTOMATIC EDIT (latexlist): Replaced 175 formulas out of 189 by TEX code with an average confidence of 2.0 and a minimal confidence of 2.0.) |
|||
| Line 1: | Line 1: | ||
| + | <!--This article has been texified automatically. Since there was no Nroff source code for this article, | ||
| + | the semi-automatic procedure described at https://encyclopediaofmath.org/wiki/User:Maximilian_Janisch/latexlist | ||
| + | was used. | ||
| + | If the TeX and formula formatting is correct, please remove this message and the {{TEX|semi-auto}} category. | ||
| + | |||
| + | Out of 189 formulas, 175 were replaced by TEX code.--> | ||
| + | |||
| + | {{TEX|semi-auto}}{{TEX|partial}} | ||
Algebraic logic can be divided into two major parts: abstract (or universal) algebraic logic and "concrete" algebraic logic (or algebras of relations of various ranks). Both are discussed below. | Algebraic logic can be divided into two major parts: abstract (or universal) algebraic logic and "concrete" algebraic logic (or algebras of relations of various ranks). Both are discussed below. | ||
==Abstract algebraic logic== | ==Abstract algebraic logic== | ||
| − | This branch of algebraic logic is built around a duality theory which associates, roughly speaking, quasi-varieties of algebras to logical systems (logics for short) and vice versa. After the duality theory is elaborated, characterization theorems follow, characterizing distinguished logical properties of a logic | + | This branch of algebraic logic is built around a duality theory which associates, roughly speaking, quasi-varieties of algebras to logical systems (logics for short) and vice versa. After the duality theory is elaborated, characterization theorems follow, characterizing distinguished logical properties of a logic $L$ in terms of natural algebraic properties of the algebraic counterpart $\operatorname {Alg}( L )$ of $L$. |
A logic is, usually, a tuple | A logic is, usually, a tuple | ||
| − | + | \begin{equation*} \mathcal{L} = \langle \operatorname{Fm} _ { \mathcal{L} } , \operatorname { Mod } _ { \mathcal{L} } , \vDash _ { \mathcal{L} } , \operatorname { mng } _ { \mathcal{L} } , \vdash _ { \mathcal{L} } \rangle , \end{equation*} | |
| − | where | + | where $\operatorname {Fm}$ is the set of formulas of $\mathcal{L}$, $\operatorname{Mod}$ is the class of models of $\mathcal{L}$, $\models _ { \mathcal{L} } \subseteq \operatorname{Mod} \times \operatorname{Fm}$ is the validity relation, $\operatorname{mng} : \operatorname{Mod} \times \operatorname{Fm} \rightarrow \operatorname{Sets}$ is the semantical meaning (or denotation) function of $\mathcal{L}$, and $\vdash$ is the syntactical provability relation of $\mathcal{L}$. |
| − | More generally, a general logic consists of a class | + | More generally, a general logic consists of a class $\operatorname{Voc}_\mathcal{L}$ of vocabularies and then to each vocabulary $\tau \in \operatorname {Voc}_{\mathcal{L}}$, $\mathcal{L}$ associates a logic, i.e. a $5$-tuple $\mathcal{L} ( \tau ) = \langle \operatorname { Fm} _ { \tau } , \operatorname { Mod} _ { \tau } , \models _ { \tau } , \operatorname { mng} _ { \tau } , \vdash _ { \tau } \rangle$ as indicated above. As an example, first-order logic is a general logic in the sense that to any collection of predicate symbols it associates a concrete first-order language built up from those predicate symbols (i.e. that vocabulary; cf. also [[Mathematical logic|Mathematical logic]]). |
| − | Of course, there are some conditions which logics and general logics have to satisfy, otherwise any "crazy" odd | + | Of course, there are some conditions which logics and general logics have to satisfy, otherwise any "crazy" odd $5$-tuple would count as a logic, which one wants to avoid. (E.g., one assumes that if $\Gamma \vdash_{\mathcal{ L}} \phi$ and $\Gamma \subseteq \Delta$, then $\Delta H \vdash_{\mathcal{L}} \phi $, for $\Gamma , \Delta \subseteq \text{Fm} _ { \mathcal{L} }$.) For such conditions on logics and general logics, see [[#References|[a4]]], [[#References|[a27]]], [[#References|[a24]]], or, for the case of logics without semantics (i.e. without $\operatorname{Mod}_{\cal L}$), [[#References|[a7]]]. These conditions go back to pioneering papers of A. Tarski, cf. [[#References|[a34]]]. |
| − | To each logic and general logic there is associated a set | + | To each logic and general logic there is associated a set $\operatorname {Cnn} _ { \mathcal{L} }$ of logical connectives, specified in such a way that $\operatorname{Fm} _ { \cal L }$ or $\operatorname{Fm} _ { \tau }$ becomes an absolutely free algebra (cf. also [[Free algebra|Free algebra]]) generated by the atomic formulas of $\tau$ and $\mathcal{L}$ and using $\operatorname {Cnn} _ { \mathcal{L} }$ as algebraic operations. Hence one can view $\operatorname {Cnn} _ { \mathcal{L} }$ as the similarity type of the algebras $\operatorname{Fm} _ { \tau }$. Using the algebras $\operatorname{Fm} _ { \tau }$ and the provability relation $\vdash _ { \tau }$, one can associate a class $\textbf{Alg} _ { \vdash } ( \mathcal{L} )$ of algebras to $\mathcal{L}$. Each of these algebras corresponds to a syntactical theory of $\mathcal{L}$. Using $\operatorname{Fm} _ { \tau }$ together with $\operatorname{mng}_ \tau$ and $\models_{\tau} $, one can associate a second class ${\bf Alg}_\models ( {\cal L} )$ of algebras to $\mathcal{L}$. ${\bf Alg}_\models ( {\cal L} )$ represents semantical aspects of $\mathcal{L}$, e.g. each model $\mathfrak{M} \in \operatorname{Mod}_{\tau}$ corresponds to an algebra in ${\bf Alg}_\models ( {\cal L} )$. Often, the members of ${\bf Alg}_\models ( {\cal L} )$ are called representable algebras or meaning algebras of $\mathcal{L}$. Under mild conditions on $\mathcal{L}$, one can prove that $\textbf{Alg} _ { \vdash } ( \mathcal{L} )$ is a [[Quasi-variety|quasi-variety]] and that $\textbf{Alg} _ { \vDash } ( \mathcal{L} ) \subseteq \textbf{Alg} _ { \vdash } ( \mathcal{L} )$. If the logic $\mathcal{L}$ is complete, then $ \mathbf{SP\mathsf{Alg}} _{\models}( \mathcal{L} ) = \mathbf{SP\mathsf{Alg}} _ { \vdash } ( \mathcal{L} )$, cf. e.g. [[#References|[a4]]]. |
===Examples.=== | ===Examples.=== | ||
| − | If | + | If $\mathcal{L}$ is propositional logic (cf. also [[Mathematical logic|Mathematical logic]]; [[Propositional calculus|Propositional calculus]]), then $\mathbf{\mathsf{Alg}} _ { \vdash } ( \mathcal{L} ) = \mathbf{\mathsf{Alg}}_ { \models } ( \mathcal{L} )$ is the class $\mathsf{BA}$ of Boolean algebras (cf. [[Boolean algebra|Boolean algebra]]). Let $n \in \omega$. For the $n$-variable fragment $L_{n}$ of first-order logic, $\mathbf{\mathsf{Alg}} _ {\vdash } ( L _ { n } )$ is the class ${\bf C A} _ { n }$ of cylindric algebras of dimension $n$, while ${\bf Alg}_\models( L _ { n } )$ is the class $\mathbf{\mathsf{RCA}}_n$ of representable cylindric algebras. For a certain variant $L _ { w }$ of first-order logic, $\textbf{Alg}_{ \vdash } ( L _ { \omega } )$ is the class $\mathbf{\mathsf{RCA}}_{ \omega}$ of representable $\mathsf{CA} _ { \omega }$s. $L _ { w }$ is called the full restricted first-order language in [[#References|[a11]]], Vol. II, cf. also [[#References|[a4]]], § 6, and [[#References|[a7]]], Appendix C. For the algebraic counterparts of other logics (as well as other versions of first-order logic), see [[#References|[a4]]]. |
| − | Now, take the logic | + | Now, take the logic $L_{n}$ as an example. The algebraic counterparts of theories of $L_{n}$ are exactly the algebras in ${\bf C A} _ { n }$ and the interpretations between theories correspond exactly to the homomorphisms between ${\bf C A} _ { n }$s. Further, axiomatizable classes of models of $L_{n}$ correspond to $\mathbf{\mathsf{RCA}}_n$s and (semantic) interpretations between such classes of models correspond to special homomorphisms, called base-homomorphisms, between $\mathbf{\mathsf{RCA}}_n$s, cf. [[#References|[a11]]], Vol. II, p. 170. Individual models of $L_{n}$ correspond to simple $\mathbf{\mathsf{RCA}}_n$s and elementary equivalence of models corresponds to isomorphism of $\mathbf{\mathsf{RCA}}_n$s. The elements of an $\mathbf{\mathsf{RCA}}_n$ corresponding to a model $\mathfrak{M}$ are best thought of as the relations definable in $\mathfrak{M}$. |
Of the duality theory between logics and their algebraic counterparts only the translation | Of the duality theory between logics and their algebraic counterparts only the translation | ||
| − | + | \begin{equation*} {\bf Alg} : \text{ ''logics"}\to \text{''pairs of classes of algebras"} \end{equation*} | |
| − | was discussed above. The other direction can also be elaborated (and then a two-sided duality like Stone duality between | + | was discussed above. The other direction can also be elaborated (and then a two-sided duality like Stone duality between $\mathsf{BA}$s and certain topological spaces can occur; cf. also [[Stone space|Stone space]]); see [[#References|[a7]]], p.21, for more on such a two-sided duality between logics and quasi-varieties of algebras. |
===Some equivalence theorems.=== | ===Some equivalence theorems.=== | ||
| − | Using the duality theory outlined above, logical properties of | + | Using the duality theory outlined above, logical properties of $\mathcal{L}$ can be characterized by algebraic properties of ${\bf Alg}_\models ( {\cal L} )$, $\textbf{Alg} _ { \vdash } ( \mathcal{L} )$ (under some mild assumptions on $\mathcal{L}$). E.g. the deduction property of $\mathcal{L}$ is equivalent with $\textbf{Alg} _ { \vdash } ( \mathcal{L} )$ having equationally definable principal congruences. The Beth definability property for $\mathcal{L}$ is equivalent with surjectiveness of all epimorphisms in ${\bf Alg}_\models ( {\cal L} )$. The various definability properties (weak Beth, local Beth, etc.) and interpolation properties are equivalent with distinguished versions of the amalgamation property and surjectiveness of epimorphisms, respectively, in $\textbf{Alg} _ { \vdash } ( \mathcal{L} )$ or ${\bf Alg}_\models ( {\cal L} )$. A kind of completeness theorem for $\mathcal{L}$ is equivalent with finite axiomatizability of ${\bf Alg}_\models ( {\cal L} )$. Compactness of $\mathcal{L}$ is equivalent with ${\bf Alg}_\models ( {\cal L} )$ being closed under ultraproducts. The above (and further) equivalence theorems are elaborated in e.g. [[#References|[a4]]]. Further such results can be found in e.g. [[#References|[a11]]], [[#References|[a7]]], [[#References|[a22]]], [[#References|[a23]]], [[#References|[a31]]], [[#References|[a14]]], [[#References|[a21]]], [[#References|[a19]]], work of J. Czelakowski, L. Maksimova, and the references in [[#References|[a35]]]. A duality theory for algebraic logic is in [[#References|[a8]]]. An overview of duality theories is in [[#References|[a2]]], Chap. 6. |
==Concrete algebraic logic.== | ==Concrete algebraic logic.== | ||
| − | This branch investigates classes of algebras that arise in the algebraization of the most frequently used logics. Below, attention is restricted to algebras of classical quantifier logics, algebras of the finite variable fragments | + | This branch investigates classes of algebras that arise in the algebraization of the most frequently used logics. Below, attention is restricted to algebras of classical quantifier logics, algebras of the finite variable fragments $L_{n}$ of these logics, relativized versions of these logics, e.g. the guarded fragment, and logics of the dynamic trend, whose algebras are relation algebras or relativized relation algebras. See also [[Abstract algebraic logic|Abstract algebraic logic]]. The objective is to "algebraize" logics which extend classical propositional logic. The algebras of this propositional logic are Boolean algebras (cf. also [[Boolean algebra|Boolean algebra]]). Boolean algebras are natural algebras of unary relations. One expects the algebras of the extended logics to be extensions of Boolean algebras to algebras of relations of higher ranks. The elements of a Boolean algebra are sets of points; one expects the elements of the new algebras to be sets of sequences (since relations are sets of sequences). |
| − | + | $n$-ary representable cylindric algebras ($\mathbf{\mathsf{RCA}}_n$s) are algebras of $n$-ary relations. They correspond to the $n$-variable fragment $L_{n}$ of first-order logic. The new operations are cylindrifications $c_{i}$ ($\dot { i } < n$). If $R \subseteq \square ^ { n } U$ is a relation defined by a formula $\varphi ( v_ { 0 } , \dots , v _ { n - 1} )$, then $c _ { i } ( R ) \subseteq \square ^ { n } U$ is the relation defined by the formula $\exists v _ { i } \varphi ( v _ { 0 } , \dots , v _ { n - 1} )$. (To be precise, one should write $c _ { i } ^ { U }$ for $c_{i}$.) Assume $n = 2$, $R \subseteq U \times U$. Then $\operatorname { c }_{0} ( R ) = U \times \operatorname { Rng } ( R )$ and $c _ { 1 } ( R ) = \operatorname { Dom } ( R ) \times U$. This shows that $c_{i}$ is a natural and simple operation on $n$-ary relations: it simply abstracts from the $i$th argument of the relation. Let $\dot { i } < n$, $R \subseteq \square ^ { n } U$. Then | |
| − | + | \begin{equation*} c _ { i } ( R ) = \end{equation*} | |
| − | + | \begin{equation*} = \{ \langle b _ { 0 } , \dots , b _ { i - 1} , a , b _ { i + 1} , \dots , b _ { n - 1 } \rangle : a \in U \ \text{and} \end{equation*} | |
| − | + | \begin{equation*} \exists b _ { i } : b = \langle b _ { 0 } , \dots , b _ { i - 1} , b _ { i } , b _ { i + 1} , \dots , b _ { n - 1} \rangle \in R \}. \end{equation*} | |
| − | In other words, if | + | In other words, if $\pi _ { i } : \square ^ { n } U \rightarrow \square ^ { ( n - 1 ) } U$ is the canonical projection along the $i$th factor, then |
| − | + | \begin{equation*} c _ { i } ( R ) = \pi _ { i } ^ { - 1 } \pi _ { i } ( ( R ) ). \end{equation*} | |
| − | + | $\mathfrak { P } ( U ) = \langle \mathcal{P} ( U ) , \cap , \cup , - \rangle$ denotes the Boolean algebra of all subsets of $U$. The algebra of $n$-ary relations over $U$ is | |
| − | + | \begin{equation*} \mathfrak { Rel } _ { n } ( U ) = \left( \mathfrak { P } ( \square ^ { n } U ) , c _ { 0 } , \ldots , c _ { n - 1} , \operatorname{Id} \right) \end{equation*} | |
| − | where the constant operation | + | where the constant operation $\operatorname{Id}$ is the $n$-ary identity relation, $\operatorname {Id} = \{ \langle a , \ldots , a \rangle : a \in U \}$ over $U$. E.g. the smallest subalgebra of $\mathfrak{Rel}_2( U )$ has $\leq 2$ atoms, while that of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a130/a130180/a130180141.png"/> has $\leq 2 ^ { ( n ^ { 2 } ) }$ atoms. The class $\mathbf{\mathsf{RCA}}_n$ of $n$-ary representable cylindric algebras is defined as |
| − | + | \begin{equation*} \mathbf{\mathsf{RCA}} _ { n } = \mathbf{SP} \{ \mathfrak{Rel} _ { n } ( U ) : U \ \text {is a set } \}, \end{equation*} | |
| − | where | + | where $\mathbf{S}$ and $\bf P$ are the operators on classes of algebras corresponding to taking isomorphs of subalgebras and direct products, respectively. |
| − | Let | + | Let $n > 2$. Then $\mathbf{\mathsf{RCA}}_n$ is a discriminator variety, with an undecidable but recursively enumerable equational theory. $\mathbf{\mathsf{RCA}}_n$ is not finitely axiomatizable, fails to have almost any form of the amalgamation property and has non-surjective epimorphisms. Almost all of these theorems remain true if one throws away the constant $\operatorname{Id}$ (from $\mathbf{\mathsf{RCA}}_n$) and closes up under $\mathbf{S}$ to make it a universally axiomatizable class. These properties imply theorems about $L_{n}$ via the duality theory between logics and classes of algebras elaborated in [[Abstract algebraic logic|abstract algebraic logic]]. Further, usual [[Set theory|set theory]] can be built up in $L_3$ (and even in the equational theory of ${\bf C A} _ { 3 }$). Hence $L_3$ (and ${\bf C A} _ { 3 }$) have the "Gödel incompleteness property" , cf. [[#References|[a28]]] and also [[Gödel incompleteness theorem|Gödel incompleteness theorem]]. |
| − | For first-order logic | + | For first-order logic $L _ { w }$ with infinitely many variables (cf. e.g. [[#References|[a7]]], Appendix C), the algebraic counterpart is $\mathbf{\mathsf{RCA}}_{ \omega}$ (algebras of $\omega$-ary relations). To generalize $\mathbf{\mathsf{RCA}}_n$ to $\mathbf{\mathsf{RCA}}_{ \omega}$, one needs only a single non-trivial step: one has to brake up the single constant $\operatorname{Id}$ to a set of constants $\operatorname {Id} _ { i j } = \{ q \in \square ^ { \omega } U : q_i = q_j \}$, with $i , j \in \omega$. Now |
| − | + | \begin{equation*} \mathbf{\mathsf{RCA}} _ { \omega } = \mathbf{SP} \left\{ \left( \mathfrak { P } ( \square ^ { \omega } U ) , c _ { i } , \operatorname{Id} _ { i j } \right)_ { i ,\, j \in \omega } : U \ \text {is a set } \right\}. \end{equation*} | |
| − | The definition of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a130/a130180/a130180169.png" /> with | + | The definition of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a130/a130180/a130180169.png"/> with $\alpha$ an arbitrary [[Ordinal number|ordinal number]] is practically the same. <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a130/a130180/a130180171.png"/> is an arithmetical variety, not axiomatizable by any set $\Sigma$ of formulas involving only finitely many individual variables. Most of the theorems about $\mathbf{\mathsf{RCA}}_n$ mentioned above carry over to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a130/a130180/a130180174.png"/>. |
| − | The greatest element of a "generic" <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a130/a130180/a130180175.png" /> was required to be a Cartesian space | + | The greatest element of a "generic" <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a130/a130180/a130180175.png"/> was required to be a Cartesian space $\square ^ { \alpha } U$. If one removes this condition and replaces $\square ^ { \alpha } U$ with an arbitrary $\alpha$-ary relation $V \subseteq \square ^ { \alpha } U$ in the definition, one obtains the important generalization <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a130/a130180/a130180180.png"/> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a130/a130180/a130180181.png"/>. Many of the negative properties of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a130/a130180/a130180182.png"/> disappear in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a130/a130180/a130180183.png"/>. E.g., the equational theory is decidable, is a variety generated by its finite members, enjoys the super-amalgamation property (hence the strong amalgamation property (SAP), too), etc. Logic applications of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a130/a130180/a130180184.png"/> abound, cf. e.g. [[#References|[a5]]], [[#References|[a37]]], [[#References|[a10]]], [[#References|[a26]]], [[#References|[a18]]]. |
| − | Since <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a130/a130180/a130180185.png" /> is not finite schema axiomatizable, a finitely schematizable approximation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a130/a130180/a130180186.png" /> was introduced by Tarski. There are theorems to the effect that | + | Since <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a130/a130180/a130180185.png"/> is not finite schema axiomatizable, a finitely schematizable approximation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a130/a130180/a130180186.png"/> was introduced by Tarski. There are theorems to the effect that $\bf C A$s approximate $\mathsf{RCA}$s well, cf. [[#References|[a11]]], Vol. II, §3.2, [[#References|[a25]]]. |
| − | The above illustrates the flavour of the theory of algebras of relations; important kinds of algebras not mentioned include relation algebras and quasi-polyadic algebras, cf. e.g. [[#References|[a11]]], Vol. II, [[#References|[a33]]], [[#References|[a9]]], [[#References|[a4]]], [[#References|[a30]]], [[#References|[a29]]], [[#References|[a13]]]. The theory of the latter two is analogous with that of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a130/a130180/a130180189.png" />s. Common generalizations of | + | The above illustrates the flavour of the theory of algebras of relations; important kinds of algebras not mentioned include relation algebras and quasi-polyadic algebras, cf. e.g. [[#References|[a11]]], Vol. II, [[#References|[a33]]], [[#References|[a9]]], [[#References|[a4]]], [[#References|[a30]]], [[#References|[a29]]], [[#References|[a13]]]. The theory of the latter two is analogous with that of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a130/a130180/a130180189.png"/>s. Common generalizations of $\bf C A$s, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a130/a130180/a130180191.png"/>s, relation algebras, polycyclic algebras, and their variants is the important class of Boolean algebras with operators, cf., e.g., [[#References|[a16]]], [[#References|[a8]]], [[#References|[a15]]], [[#References|[a34]]], [[#References|[a1]]], [[#References|[a17]]]. For category-theoretic approaches, see [[#References|[a4]]] and the references therein. |
| − | There are many open problems in this area (cf. e.g. [[#References|[a30]]], [[#References|[a12]]], [[#References|[a3]]], pp. 727–745, [[#References|[a32]]]). To mention one (open as of 2000): is there a variety | + | There are many open problems in this area (cf. e.g. [[#References|[a30]]], [[#References|[a12]]], [[#References|[a3]]], pp. 727–745, [[#References|[a32]]]). To mention one (open as of 2000): is there a variety $V \subseteq {\sf C A}_\alpha$ having the strong amalgamation property (SAP) but not the super-amalgamation property? |
Application areas of algebraic logic range from logic and linguistics through cognitive science, to even relativity theory, cf., e.g., the work of the Amsterdam school [[#References|[a6]]], [[#References|[a36]]], [[#References|[a20]]], [[#References|[a37]]], and [[#References|[a2]]]. | Application areas of algebraic logic range from logic and linguistics through cognitive science, to even relativity theory, cf., e.g., the work of the Amsterdam school [[#References|[a6]]], [[#References|[a36]]], [[#References|[a20]]], [[#References|[a37]]], and [[#References|[a2]]]. | ||
| Line 76: | Line 84: | ||
====References==== | ====References==== | ||
| − | <table>< | + | <table><tr><td valign="top">[a1]</td> <td valign="top"> H. Andréka, S. Givant, Sz. Mikulás, I. Németi, A. Simon, "Notions of density that imply representability in algebraic logic" ''Ann. Pure Appl. Logic'' , '''91''' (1998) pp. 93–190</td></tr><tr><td valign="top">[a2]</td> <td valign="top"> H. Andréka, J.X. Madarász, I. Németi, "On the logical structure of relativity theories" , A. Rényi Inst. Math. (2001) (www.math-inst.hu/pub/algebraic-logic)</td></tr><tr><td valign="top">[a3]</td> <td valign="top"> "Algebraic logic (Proc. Conf. Budapest 1988)" H. Andréka (ed.) J.D. Monk (ed.) I. Németi (ed.) , ''Colloq. Math. Soc. J. Bolyai'' , '''54''' , North-Holland (1991)</td></tr><tr><td valign="top">[a4]</td> <td valign="top"> H. Andréka, I. Németi, I. Sain, "Algebraic logic" , ''Handbook of Philosophical Logic'' , '''1''' , Kluwer Acad. Publ. (2001) (www.math-inst.hu/pub/algebraic-logic)</td></tr><tr><td valign="top">[a5]</td> <td valign="top"> H. Andréka, J. van Benthem, I. Németi, "Modal languages and bounded fragments of predicate logic" ''J. Philos. Logic'' , '''27''' (1998) pp. 217–274</td></tr><tr><td valign="top">[a6]</td> <td valign="top"> "Handbook of Logic and Language" J. van Benthem (ed.) A. ter Meulen (ed.) , Elsevier (1997)</td></tr><tr><td valign="top">[a7]</td> <td valign="top"> W.J. Blok, D.L. Pigozzi, "Algebraizable logics" ''Memoirs Amer. Math. Soc.'' , '''77''' : 396 (1989)</td></tr><tr><td valign="top">[a8]</td> <td valign="top"> R. Goldblatt, "Algebraic polymodal logic: A survey" ''Logic J. IGPL'' , '''8''' : 4 (2000) pp. 393–450</td></tr><tr><td valign="top">[a9]</td> <td valign="top"> R. Hirsch, I. Hodkinson, "Relation algebras by games" , Kluwer Acad. Publ. (to appear)</td></tr><tr><td valign="top">[a10]</td> <td valign="top"> E. Hoogland, M. Marx, "Interpolation in guarded fragments" ''Studia Logica'' (2000)</td></tr><tr><td valign="top">[a11]</td> <td valign="top"> L. Henkin, J.D. Monk, A. Tarski, "Cylindric algebras" , '''I—II''' , North-Holland (1971/85)</td></tr><tr><td valign="top">[a12]</td> <td valign="top"> L. Henkin, J.D. Monk, A. Tarski, H. Andréka, I. Németi, "Cylindric set algebras" , ''Lecture Notes in Math.'' , '''883''' , Springer (1981)</td></tr><tr><td valign="top">[a13]</td> <td valign="top"> "Handbook on the heart of algebra" R.A. Mikhalev (ed.) G.F. Pilz (ed.) , Kluwer Acad. Publ. (to appear)</td></tr><tr><td valign="top">[a14]</td> <td valign="top"> E. Hoogland, "Algebraic characterizations of various Beth definability properties" ''Studia Logica'' , '''65''' : 1 (2000) pp. 91–112</td></tr><tr><td valign="top">[a15]</td> <td valign="top"> P. Jipsen, B. Jónsson, J. Rafter, "Adjoining units to residuated Boolean algebras" ''Algebra Univ.'' , '''34''' : 2 (1995) pp. 118–127</td></tr><tr><td valign="top">[a16]</td> <td valign="top"> B. Jónsson, A. Tarski, "Boolean algebras with operators" , ''Alfred Tarski Collected Papers'' , '''3''' , Birkhäuser (1986)</td></tr><tr><td valign="top">[a17]</td> <td valign="top"> Á. Kurucz, "Decision problems in algebraic logic" ''PhD Diss., Budapest'' (1997) (www.math-inst.hu/pub/algebraic-logic)</td></tr><tr><td valign="top">[a18]</td> <td valign="top"> "Arrow logic and multi-modal logic" M. Marx (ed.) L. Pólos (ed.) M. Masuch (ed.) , CSLI Publ. (1996)</td></tr><tr><td valign="top">[a19]</td> <td valign="top"> J.X. Madarász, T. Sayed-Ahmed, "Amalgamation, interpolation and epimorphisms, solutions to all problems of Pigozzi's paper, and some more" ''A. Rényi Inst. Math.'' (2001)</td></tr><tr><td valign="top">[a20]</td> <td valign="top"> M. Marx, Y. Venema, "Multi-dimensional modal logic" , Kluwer Acad. Publ. (1997)</td></tr><tr><td valign="top">[a21]</td> <td valign="top"> J.X. Madarász, "Surjectiveness of epimorphisms in varieties of algebraic logic" ''Preprint A. Rényi Inst. Math.'' (2000)</td></tr><tr><td valign="top">[a22]</td> <td valign="top"> J.X. Madarász, "Interpolation and amalgamation: Pushing the limits (I)" ''Studia Logica'' , '''61''' : 3 (1998) pp. 311–345</td></tr><tr><td valign="top">[a23]</td> <td valign="top"> J.X. Madarász, "Interpolation and amalgamation: Pushing the limits (II)" ''Studia Logica'' , '''62''' : 1 (1999) pp. 1–19</td></tr><tr><td valign="top">[a24]</td> <td valign="top"> N. Marti-Oliet, J. Meseguer, "General logics and logical frameworks" D.M. Gabbay (ed.) , ''What is a Logical System'' , Clarendon Press (1994) pp. 355–392</td></tr><tr><td valign="top">[a25]</td> <td valign="top"> J.D. Monk, "An introduction to cylindric set algebras" ''Logic J. IGPL'' , '''8''' : 4 (2000) pp. 451–506</td></tr><tr><td valign="top">[a26]</td> <td valign="top"> I. Németi, "Fine-structure analysis of first order logic" M. Marx (ed.) L. Pólos (ed.) M. Masuch (ed.) , ''Arrow Logic and Multi-Modal Logic'' , CSLI Publ. (1996) pp. 221–247</td></tr><tr><td valign="top">[a27]</td> <td valign="top"> I. Németi, H. Andréka, "General algebraic logic: A perspective on what is logic" D.M. Gabbay (ed.) , ''What is a Logical System'' , Clarendon Press (1994) pp. 393–444</td></tr><tr><td valign="top">[a28]</td> <td valign="top"> I. Németi, "Logic with three variables has Gödel's incompleteness property—thus free cylindric algebras are not atomic" ''Manuscript Math. Inst. Hungar. Acad. Sci., Budapest'' (1986)</td></tr><tr><td valign="top">[a29]</td> <td valign="top"> "Special issue on Algebraic Logic" I. Németi (ed.) I. Sain (ed.) ''Logic J. IGPL'' , '''8''' : 4 (2000) (I. Nemeti and I. Sain)</td></tr><tr><td valign="top">[a30]</td> <td valign="top"> I. Németi, "Algebraization of quantifier logics, an introductory overview" ''Studia Logica'' , '''50''' : 3/4 (1991) pp. 485–570 (Special issue devoted to Algebraic Logic, eds.: W.J. Blok and D.L. Pigozzi. This is a preliminary, short version (without proofs, etc.) of www.math-inst.hu/pub/algebraic-logic)</td></tr><tr><td valign="top">[a31]</td> <td valign="top"> D.L. Pigozzi, "Amalgamation, congruence-extensions, and interpolation properties in algebras" ''Algebra Univ.'' , '''1''' : 3 (1972) pp. 269–349</td></tr><tr><td valign="top">[a32]</td> <td valign="top"> A. Simon, "Non-representable algebras of relations" ''PhD Diss., Budapest'' (1997) (www.math-inst.hu/pub/algebraic-logic)</td></tr><tr><td valign="top">[a33]</td> <td valign="top"> A. Tarski, S. Givant, "A formalization of set theory without variables" , ''Colloq. Publ.'' , '''41''' , Amer. Math. Soc. (1987)</td></tr><tr><td valign="top">[a34]</td> <td valign="top"> S.R. Givant (ed.) R.N. McKenzie (ed.) , ''Alfred Tarski: Collected Works'' , '''1–4''' , Birkhäuser (1986) (S.R. Givant and R.N. McKenzie)</td></tr><tr><td valign="top">[a35]</td> <td valign="top"> "Special issue on abstract algebraic logic" J.M. Font (ed.) R. Jansana (ed.) D. Pigozzi (ed.) ''Studia Logica'' , '''65''' : 1 (2000) (J.M. Font and R. Jansana and D. Pigozzi)</td></tr><tr><td valign="top">[a36]</td> <td valign="top"> J. van Benthem, "Language in action (categories, lambdas and dynamic logic)" , ''Studies in Logic'' , '''130''' , North-Holland (1991)</td></tr><tr><td valign="top">[a37]</td> <td valign="top"> J.A.F.K. van Benthem, "Exploring logical dynamics" , ''Studies in Logic, Language and Information'' , CSLI Publ. (1996)</td></tr></table> |
Revision as of 17:02, 1 July 2020
Algebraic logic can be divided into two major parts: abstract (or universal) algebraic logic and "concrete" algebraic logic (or algebras of relations of various ranks). Both are discussed below.
Abstract algebraic logic
This branch of algebraic logic is built around a duality theory which associates, roughly speaking, quasi-varieties of algebras to logical systems (logics for short) and vice versa. After the duality theory is elaborated, characterization theorems follow, characterizing distinguished logical properties of a logic $L$ in terms of natural algebraic properties of the algebraic counterpart $\operatorname {Alg}( L )$ of $L$.
A logic is, usually, a tuple
\begin{equation*} \mathcal{L} = \langle \operatorname{Fm} _ { \mathcal{L} } , \operatorname { Mod } _ { \mathcal{L} } , \vDash _ { \mathcal{L} } , \operatorname { mng } _ { \mathcal{L} } , \vdash _ { \mathcal{L} } \rangle , \end{equation*}
where $\operatorname {Fm}$ is the set of formulas of $\mathcal{L}$, $\operatorname{Mod}$ is the class of models of $\mathcal{L}$, $\models _ { \mathcal{L} } \subseteq \operatorname{Mod} \times \operatorname{Fm}$ is the validity relation, $\operatorname{mng} : \operatorname{Mod} \times \operatorname{Fm} \rightarrow \operatorname{Sets}$ is the semantical meaning (or denotation) function of $\mathcal{L}$, and $\vdash$ is the syntactical provability relation of $\mathcal{L}$.
More generally, a general logic consists of a class $\operatorname{Voc}_\mathcal{L}$ of vocabularies and then to each vocabulary $\tau \in \operatorname {Voc}_{\mathcal{L}}$, $\mathcal{L}$ associates a logic, i.e. a $5$-tuple $\mathcal{L} ( \tau ) = \langle \operatorname { Fm} _ { \tau } , \operatorname { Mod} _ { \tau } , \models _ { \tau } , \operatorname { mng} _ { \tau } , \vdash _ { \tau } \rangle$ as indicated above. As an example, first-order logic is a general logic in the sense that to any collection of predicate symbols it associates a concrete first-order language built up from those predicate symbols (i.e. that vocabulary; cf. also Mathematical logic).
Of course, there are some conditions which logics and general logics have to satisfy, otherwise any "crazy" odd $5$-tuple would count as a logic, which one wants to avoid. (E.g., one assumes that if $\Gamma \vdash_{\mathcal{ L}} \phi$ and $\Gamma \subseteq \Delta$, then $\Delta H \vdash_{\mathcal{L}} \phi $, for $\Gamma , \Delta \subseteq \text{Fm} _ { \mathcal{L} }$.) For such conditions on logics and general logics, see [a4], [a27], [a24], or, for the case of logics without semantics (i.e. without $\operatorname{Mod}_{\cal L}$), [a7]. These conditions go back to pioneering papers of A. Tarski, cf. [a34].
To each logic and general logic there is associated a set $\operatorname {Cnn} _ { \mathcal{L} }$ of logical connectives, specified in such a way that $\operatorname{Fm} _ { \cal L }$ or $\operatorname{Fm} _ { \tau }$ becomes an absolutely free algebra (cf. also Free algebra) generated by the atomic formulas of $\tau$ and $\mathcal{L}$ and using $\operatorname {Cnn} _ { \mathcal{L} }$ as algebraic operations. Hence one can view $\operatorname {Cnn} _ { \mathcal{L} }$ as the similarity type of the algebras $\operatorname{Fm} _ { \tau }$. Using the algebras $\operatorname{Fm} _ { \tau }$ and the provability relation $\vdash _ { \tau }$, one can associate a class $\textbf{Alg} _ { \vdash } ( \mathcal{L} )$ of algebras to $\mathcal{L}$. Each of these algebras corresponds to a syntactical theory of $\mathcal{L}$. Using $\operatorname{Fm} _ { \tau }$ together with $\operatorname{mng}_ \tau$ and $\models_{\tau} $, one can associate a second class ${\bf Alg}_\models ( {\cal L} )$ of algebras to $\mathcal{L}$. ${\bf Alg}_\models ( {\cal L} )$ represents semantical aspects of $\mathcal{L}$, e.g. each model $\mathfrak{M} \in \operatorname{Mod}_{\tau}$ corresponds to an algebra in ${\bf Alg}_\models ( {\cal L} )$. Often, the members of ${\bf Alg}_\models ( {\cal L} )$ are called representable algebras or meaning algebras of $\mathcal{L}$. Under mild conditions on $\mathcal{L}$, one can prove that $\textbf{Alg} _ { \vdash } ( \mathcal{L} )$ is a quasi-variety and that $\textbf{Alg} _ { \vDash } ( \mathcal{L} ) \subseteq \textbf{Alg} _ { \vdash } ( \mathcal{L} )$. If the logic $\mathcal{L}$ is complete, then $ \mathbf{SP\mathsf{Alg}} _{\models}( \mathcal{L} ) = \mathbf{SP\mathsf{Alg}} _ { \vdash } ( \mathcal{L} )$, cf. e.g. [a4].
Examples.
If $\mathcal{L}$ is propositional logic (cf. also Mathematical logic; Propositional calculus), then $\mathbf{\mathsf{Alg}} _ { \vdash } ( \mathcal{L} ) = \mathbf{\mathsf{Alg}}_ { \models } ( \mathcal{L} )$ is the class $\mathsf{BA}$ of Boolean algebras (cf. Boolean algebra). Let $n \in \omega$. For the $n$-variable fragment $L_{n}$ of first-order logic, $\mathbf{\mathsf{Alg}} _ {\vdash } ( L _ { n } )$ is the class ${\bf C A} _ { n }$ of cylindric algebras of dimension $n$, while ${\bf Alg}_\models( L _ { n } )$ is the class $\mathbf{\mathsf{RCA}}_n$ of representable cylindric algebras. For a certain variant $L _ { w }$ of first-order logic, $\textbf{Alg}_{ \vdash } ( L _ { \omega } )$ is the class $\mathbf{\mathsf{RCA}}_{ \omega}$ of representable $\mathsf{CA} _ { \omega }$s. $L _ { w }$ is called the full restricted first-order language in [a11], Vol. II, cf. also [a4], § 6, and [a7], Appendix C. For the algebraic counterparts of other logics (as well as other versions of first-order logic), see [a4].
Now, take the logic $L_{n}$ as an example. The algebraic counterparts of theories of $L_{n}$ are exactly the algebras in ${\bf C A} _ { n }$ and the interpretations between theories correspond exactly to the homomorphisms between ${\bf C A} _ { n }$s. Further, axiomatizable classes of models of $L_{n}$ correspond to $\mathbf{\mathsf{RCA}}_n$s and (semantic) interpretations between such classes of models correspond to special homomorphisms, called base-homomorphisms, between $\mathbf{\mathsf{RCA}}_n$s, cf. [a11], Vol. II, p. 170. Individual models of $L_{n}$ correspond to simple $\mathbf{\mathsf{RCA}}_n$s and elementary equivalence of models corresponds to isomorphism of $\mathbf{\mathsf{RCA}}_n$s. The elements of an $\mathbf{\mathsf{RCA}}_n$ corresponding to a model $\mathfrak{M}$ are best thought of as the relations definable in $\mathfrak{M}$.
Of the duality theory between logics and their algebraic counterparts only the translation
\begin{equation*} {\bf Alg} : \text{ ''logics"}\to \text{''pairs of classes of algebras"} \end{equation*}
was discussed above. The other direction can also be elaborated (and then a two-sided duality like Stone duality between $\mathsf{BA}$s and certain topological spaces can occur; cf. also Stone space); see [a7], p.21, for more on such a two-sided duality between logics and quasi-varieties of algebras.
Some equivalence theorems.
Using the duality theory outlined above, logical properties of $\mathcal{L}$ can be characterized by algebraic properties of ${\bf Alg}_\models ( {\cal L} )$, $\textbf{Alg} _ { \vdash } ( \mathcal{L} )$ (under some mild assumptions on $\mathcal{L}$). E.g. the deduction property of $\mathcal{L}$ is equivalent with $\textbf{Alg} _ { \vdash } ( \mathcal{L} )$ having equationally definable principal congruences. The Beth definability property for $\mathcal{L}$ is equivalent with surjectiveness of all epimorphisms in ${\bf Alg}_\models ( {\cal L} )$. The various definability properties (weak Beth, local Beth, etc.) and interpolation properties are equivalent with distinguished versions of the amalgamation property and surjectiveness of epimorphisms, respectively, in $\textbf{Alg} _ { \vdash } ( \mathcal{L} )$ or ${\bf Alg}_\models ( {\cal L} )$. A kind of completeness theorem for $\mathcal{L}$ is equivalent with finite axiomatizability of ${\bf Alg}_\models ( {\cal L} )$. Compactness of $\mathcal{L}$ is equivalent with ${\bf Alg}_\models ( {\cal L} )$ being closed under ultraproducts. The above (and further) equivalence theorems are elaborated in e.g. [a4]. Further such results can be found in e.g. [a11], [a7], [a22], [a23], [a31], [a14], [a21], [a19], work of J. Czelakowski, L. Maksimova, and the references in [a35]. A duality theory for algebraic logic is in [a8]. An overview of duality theories is in [a2], Chap. 6.
Concrete algebraic logic.
This branch investigates classes of algebras that arise in the algebraization of the most frequently used logics. Below, attention is restricted to algebras of classical quantifier logics, algebras of the finite variable fragments $L_{n}$ of these logics, relativized versions of these logics, e.g. the guarded fragment, and logics of the dynamic trend, whose algebras are relation algebras or relativized relation algebras. See also Abstract algebraic logic. The objective is to "algebraize" logics which extend classical propositional logic. The algebras of this propositional logic are Boolean algebras (cf. also Boolean algebra). Boolean algebras are natural algebras of unary relations. One expects the algebras of the extended logics to be extensions of Boolean algebras to algebras of relations of higher ranks. The elements of a Boolean algebra are sets of points; one expects the elements of the new algebras to be sets of sequences (since relations are sets of sequences).
$n$-ary representable cylindric algebras ($\mathbf{\mathsf{RCA}}_n$s) are algebras of $n$-ary relations. They correspond to the $n$-variable fragment $L_{n}$ of first-order logic. The new operations are cylindrifications $c_{i}$ ($\dot { i } < n$). If $R \subseteq \square ^ { n } U$ is a relation defined by a formula $\varphi ( v_ { 0 } , \dots , v _ { n - 1} )$, then $c _ { i } ( R ) \subseteq \square ^ { n } U$ is the relation defined by the formula $\exists v _ { i } \varphi ( v _ { 0 } , \dots , v _ { n - 1} )$. (To be precise, one should write $c _ { i } ^ { U }$ for $c_{i}$.) Assume $n = 2$, $R \subseteq U \times U$. Then $\operatorname { c }_{0} ( R ) = U \times \operatorname { Rng } ( R )$ and $c _ { 1 } ( R ) = \operatorname { Dom } ( R ) \times U$. This shows that $c_{i}$ is a natural and simple operation on $n$-ary relations: it simply abstracts from the $i$th argument of the relation. Let $\dot { i } < n$, $R \subseteq \square ^ { n } U$. Then
\begin{equation*} c _ { i } ( R ) = \end{equation*}
\begin{equation*} = \{ \langle b _ { 0 } , \dots , b _ { i - 1} , a , b _ { i + 1} , \dots , b _ { n - 1 } \rangle : a \in U \ \text{and} \end{equation*}
\begin{equation*} \exists b _ { i } : b = \langle b _ { 0 } , \dots , b _ { i - 1} , b _ { i } , b _ { i + 1} , \dots , b _ { n - 1} \rangle \in R \}. \end{equation*}
In other words, if $\pi _ { i } : \square ^ { n } U \rightarrow \square ^ { ( n - 1 ) } U$ is the canonical projection along the $i$th factor, then
\begin{equation*} c _ { i } ( R ) = \pi _ { i } ^ { - 1 } \pi _ { i } ( ( R ) ). \end{equation*}
$\mathfrak { P } ( U ) = \langle \mathcal{P} ( U ) , \cap , \cup , - \rangle$ denotes the Boolean algebra of all subsets of $U$. The algebra of $n$-ary relations over $U$ is
\begin{equation*} \mathfrak { Rel } _ { n } ( U ) = \left( \mathfrak { P } ( \square ^ { n } U ) , c _ { 0 } , \ldots , c _ { n - 1} , \operatorname{Id} \right) \end{equation*}
where the constant operation $\operatorname{Id}$ is the $n$-ary identity relation, $\operatorname {Id} = \{ \langle a , \ldots , a \rangle : a \in U \}$ over $U$. E.g. the smallest subalgebra of $\mathfrak{Rel}_2( U )$ has $\leq 2$ atoms, while that of 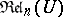 has $\leq 2 ^ { ( n ^ { 2 } ) }$ atoms. The class $\mathbf{\mathsf{RCA}}_n$ of $n$-ary representable cylindric algebras is defined as
has $\leq 2 ^ { ( n ^ { 2 } ) }$ atoms. The class $\mathbf{\mathsf{RCA}}_n$ of $n$-ary representable cylindric algebras is defined as
\begin{equation*} \mathbf{\mathsf{RCA}} _ { n } = \mathbf{SP} \{ \mathfrak{Rel} _ { n } ( U ) : U \ \text {is a set } \}, \end{equation*}
where $\mathbf{S}$ and $\bf P$ are the operators on classes of algebras corresponding to taking isomorphs of subalgebras and direct products, respectively.
Let $n > 2$. Then $\mathbf{\mathsf{RCA}}_n$ is a discriminator variety, with an undecidable but recursively enumerable equational theory. $\mathbf{\mathsf{RCA}}_n$ is not finitely axiomatizable, fails to have almost any form of the amalgamation property and has non-surjective epimorphisms. Almost all of these theorems remain true if one throws away the constant $\operatorname{Id}$ (from $\mathbf{\mathsf{RCA}}_n$) and closes up under $\mathbf{S}$ to make it a universally axiomatizable class. These properties imply theorems about $L_{n}$ via the duality theory between logics and classes of algebras elaborated in abstract algebraic logic. Further, usual set theory can be built up in $L_3$ (and even in the equational theory of ${\bf C A} _ { 3 }$). Hence $L_3$ (and ${\bf C A} _ { 3 }$) have the "Gödel incompleteness property" , cf. [a28] and also Gödel incompleteness theorem.
For first-order logic $L _ { w }$ with infinitely many variables (cf. e.g. [a7], Appendix C), the algebraic counterpart is $\mathbf{\mathsf{RCA}}_{ \omega}$ (algebras of $\omega$-ary relations). To generalize $\mathbf{\mathsf{RCA}}_n$ to $\mathbf{\mathsf{RCA}}_{ \omega}$, one needs only a single non-trivial step: one has to brake up the single constant $\operatorname{Id}$ to a set of constants $\operatorname {Id} _ { i j } = \{ q \in \square ^ { \omega } U : q_i = q_j \}$, with $i , j \in \omega$. Now
\begin{equation*} \mathbf{\mathsf{RCA}} _ { \omega } = \mathbf{SP} \left\{ \left( \mathfrak { P } ( \square ^ { \omega } U ) , c _ { i } , \operatorname{Id} _ { i j } \right)_ { i ,\, j \in \omega } : U \ \text {is a set } \right\}. \end{equation*}
The definition of 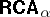 with $\alpha$ an arbitrary ordinal number is practically the same.
with $\alpha$ an arbitrary ordinal number is practically the same. 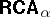 is an arithmetical variety, not axiomatizable by any set $\Sigma$ of formulas involving only finitely many individual variables. Most of the theorems about $\mathbf{\mathsf{RCA}}_n$ mentioned above carry over to
is an arithmetical variety, not axiomatizable by any set $\Sigma$ of formulas involving only finitely many individual variables. Most of the theorems about $\mathbf{\mathsf{RCA}}_n$ mentioned above carry over to 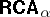 .
.
The greatest element of a "generic" 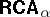 was required to be a Cartesian space $\square ^ { \alpha } U$. If one removes this condition and replaces $\square ^ { \alpha } U$ with an arbitrary $\alpha$-ary relation $V \subseteq \square ^ { \alpha } U$ in the definition, one obtains the important generalization
was required to be a Cartesian space $\square ^ { \alpha } U$. If one removes this condition and replaces $\square ^ { \alpha } U$ with an arbitrary $\alpha$-ary relation $V \subseteq \square ^ { \alpha } U$ in the definition, one obtains the important generalization 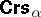 of
of 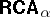 . Many of the negative properties of
. Many of the negative properties of 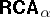 disappear in
disappear in 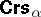 . E.g., the equational theory is decidable, is a variety generated by its finite members, enjoys the super-amalgamation property (hence the strong amalgamation property (SAP), too), etc. Logic applications of
. E.g., the equational theory is decidable, is a variety generated by its finite members, enjoys the super-amalgamation property (hence the strong amalgamation property (SAP), too), etc. Logic applications of 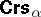 abound, cf. e.g. [a5], [a37], [a10], [a26], [a18].
abound, cf. e.g. [a5], [a37], [a10], [a26], [a18].
Since 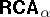 is not finite schema axiomatizable, a finitely schematizable approximation
is not finite schema axiomatizable, a finitely schematizable approximation 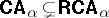 was introduced by Tarski. There are theorems to the effect that $\bf C A$s approximate $\mathsf{RCA}$s well, cf. [a11], Vol. II, §3.2, [a25].
was introduced by Tarski. There are theorems to the effect that $\bf C A$s approximate $\mathsf{RCA}$s well, cf. [a11], Vol. II, §3.2, [a25].
The above illustrates the flavour of the theory of algebras of relations; important kinds of algebras not mentioned include relation algebras and quasi-polyadic algebras, cf. e.g. [a11], Vol. II, [a33], [a9], [a4], [a30], [a29], [a13]. The theory of the latter two is analogous with that of 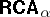 s. Common generalizations of $\bf C A$s,
s. Common generalizations of $\bf C A$s, 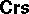 s, relation algebras, polycyclic algebras, and their variants is the important class of Boolean algebras with operators, cf., e.g., [a16], [a8], [a15], [a34], [a1], [a17]. For category-theoretic approaches, see [a4] and the references therein.
s, relation algebras, polycyclic algebras, and their variants is the important class of Boolean algebras with operators, cf., e.g., [a16], [a8], [a15], [a34], [a1], [a17]. For category-theoretic approaches, see [a4] and the references therein.
There are many open problems in this area (cf. e.g. [a30], [a12], [a3], pp. 727–745, [a32]). To mention one (open as of 2000): is there a variety $V \subseteq {\sf C A}_\alpha$ having the strong amalgamation property (SAP) but not the super-amalgamation property?
Application areas of algebraic logic range from logic and linguistics through cognitive science, to even relativity theory, cf., e.g., the work of the Amsterdam school [a6], [a36], [a20], [a37], and [a2].
This work was supported by the Hungarian National Foundation for Scientific Research T30314, T35192.
References
| [a1] | H. Andréka, S. Givant, Sz. Mikulás, I. Németi, A. Simon, "Notions of density that imply representability in algebraic logic" Ann. Pure Appl. Logic , 91 (1998) pp. 93–190 |
| [a2] | H. Andréka, J.X. Madarász, I. Németi, "On the logical structure of relativity theories" , A. Rényi Inst. Math. (2001) (www.math-inst.hu/pub/algebraic-logic) |
| [a3] | "Algebraic logic (Proc. Conf. Budapest 1988)" H. Andréka (ed.) J.D. Monk (ed.) I. Németi (ed.) , Colloq. Math. Soc. J. Bolyai , 54 , North-Holland (1991) |
| [a4] | H. Andréka, I. Németi, I. Sain, "Algebraic logic" , Handbook of Philosophical Logic , 1 , Kluwer Acad. Publ. (2001) (www.math-inst.hu/pub/algebraic-logic) |
| [a5] | H. Andréka, J. van Benthem, I. Németi, "Modal languages and bounded fragments of predicate logic" J. Philos. Logic , 27 (1998) pp. 217–274 |
| [a6] | "Handbook of Logic and Language" J. van Benthem (ed.) A. ter Meulen (ed.) , Elsevier (1997) |
| [a7] | W.J. Blok, D.L. Pigozzi, "Algebraizable logics" Memoirs Amer. Math. Soc. , 77 : 396 (1989) |
| [a8] | R. Goldblatt, "Algebraic polymodal logic: A survey" Logic J. IGPL , 8 : 4 (2000) pp. 393–450 |
| [a9] | R. Hirsch, I. Hodkinson, "Relation algebras by games" , Kluwer Acad. Publ. (to appear) |
| [a10] | E. Hoogland, M. Marx, "Interpolation in guarded fragments" Studia Logica (2000) |
| [a11] | L. Henkin, J.D. Monk, A. Tarski, "Cylindric algebras" , I—II , North-Holland (1971/85) |
| [a12] | L. Henkin, J.D. Monk, A. Tarski, H. Andréka, I. Németi, "Cylindric set algebras" , Lecture Notes in Math. , 883 , Springer (1981) |
| [a13] | "Handbook on the heart of algebra" R.A. Mikhalev (ed.) G.F. Pilz (ed.) , Kluwer Acad. Publ. (to appear) |
| [a14] | E. Hoogland, "Algebraic characterizations of various Beth definability properties" Studia Logica , 65 : 1 (2000) pp. 91–112 |
| [a15] | P. Jipsen, B. Jónsson, J. Rafter, "Adjoining units to residuated Boolean algebras" Algebra Univ. , 34 : 2 (1995) pp. 118–127 |
| [a16] | B. Jónsson, A. Tarski, "Boolean algebras with operators" , Alfred Tarski Collected Papers , 3 , Birkhäuser (1986) |
| [a17] | Á. Kurucz, "Decision problems in algebraic logic" PhD Diss., Budapest (1997) (www.math-inst.hu/pub/algebraic-logic) |
| [a18] | "Arrow logic and multi-modal logic" M. Marx (ed.) L. Pólos (ed.) M. Masuch (ed.) , CSLI Publ. (1996) |
| [a19] | J.X. Madarász, T. Sayed-Ahmed, "Amalgamation, interpolation and epimorphisms, solutions to all problems of Pigozzi's paper, and some more" A. Rényi Inst. Math. (2001) |
| [a20] | M. Marx, Y. Venema, "Multi-dimensional modal logic" , Kluwer Acad. Publ. (1997) |
| [a21] | J.X. Madarász, "Surjectiveness of epimorphisms in varieties of algebraic logic" Preprint A. Rényi Inst. Math. (2000) |
| [a22] | J.X. Madarász, "Interpolation and amalgamation: Pushing the limits (I)" Studia Logica , 61 : 3 (1998) pp. 311–345 |
| [a23] | J.X. Madarász, "Interpolation and amalgamation: Pushing the limits (II)" Studia Logica , 62 : 1 (1999) pp. 1–19 |
| [a24] | N. Marti-Oliet, J. Meseguer, "General logics and logical frameworks" D.M. Gabbay (ed.) , What is a Logical System , Clarendon Press (1994) pp. 355–392 |
| [a25] | J.D. Monk, "An introduction to cylindric set algebras" Logic J. IGPL , 8 : 4 (2000) pp. 451–506 |
| [a26] | I. Németi, "Fine-structure analysis of first order logic" M. Marx (ed.) L. Pólos (ed.) M. Masuch (ed.) , Arrow Logic and Multi-Modal Logic , CSLI Publ. (1996) pp. 221–247 |
| [a27] | I. Németi, H. Andréka, "General algebraic logic: A perspective on what is logic" D.M. Gabbay (ed.) , What is a Logical System , Clarendon Press (1994) pp. 393–444 |
| [a28] | I. Németi, "Logic with three variables has Gödel's incompleteness property—thus free cylindric algebras are not atomic" Manuscript Math. Inst. Hungar. Acad. Sci., Budapest (1986) |
| [a29] | "Special issue on Algebraic Logic" I. Németi (ed.) I. Sain (ed.) Logic J. IGPL , 8 : 4 (2000) (I. Nemeti and I. Sain) |
| [a30] | I. Németi, "Algebraization of quantifier logics, an introductory overview" Studia Logica , 50 : 3/4 (1991) pp. 485–570 (Special issue devoted to Algebraic Logic, eds.: W.J. Blok and D.L. Pigozzi. This is a preliminary, short version (without proofs, etc.) of www.math-inst.hu/pub/algebraic-logic) |
| [a31] | D.L. Pigozzi, "Amalgamation, congruence-extensions, and interpolation properties in algebras" Algebra Univ. , 1 : 3 (1972) pp. 269–349 |
| [a32] | A. Simon, "Non-representable algebras of relations" PhD Diss., Budapest (1997) (www.math-inst.hu/pub/algebraic-logic) |
| [a33] | A. Tarski, S. Givant, "A formalization of set theory without variables" , Colloq. Publ. , 41 , Amer. Math. Soc. (1987) |
| [a34] | S.R. Givant (ed.) R.N. McKenzie (ed.) , Alfred Tarski: Collected Works , 1–4 , Birkhäuser (1986) (S.R. Givant and R.N. McKenzie) |
| [a35] | "Special issue on abstract algebraic logic" J.M. Font (ed.) R. Jansana (ed.) D. Pigozzi (ed.) Studia Logica , 65 : 1 (2000) (J.M. Font and R. Jansana and D. Pigozzi) |
| [a36] | J. van Benthem, "Language in action (categories, lambdas and dynamic logic)" , Studies in Logic , 130 , North-Holland (1991) |
| [a37] | J.A.F.K. van Benthem, "Exploring logical dynamics" , Studies in Logic, Language and Information , CSLI Publ. (1996) |
Algebraic logic. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Algebraic_logic&oldid=29654