Difference between revisions of "Kolmogorov-Chapman equation"
(→References: Feller: internal link) |
(refs format) |
||
| Line 7: | Line 7: | ||
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/k/k055/k055680/k0556801.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/k/k055/k055680/k0556801.png" /></td> </tr></table> | ||
| − | that is, a condition imposed on the [[Transition function|transition function]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/k/k055/k055680/k0556802.png" /> (<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/k/k055/k055680/k0556803.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/k/k055/k055680/k0556804.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/k/k055/k055680/k0556805.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/k/k055/k055680/k0556806.png" /> being a measurable space), enabling one (under certain conditions on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/k/k055/k055680/k0556807.png" />) to construct a [[Markov process|Markov process]] for which the conditional probability <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/k/k055/k055680/k0556808.png" /> is the same as <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/k/k055/k055680/k0556809.png" />. Conversely, for a Markov process its transition function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/k/k055/k055680/k05568010.png" />, which by definition is equal to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/k/k055/k055680/k05568011.png" />, satisfies the Kolmogorov–Chapman equation, as follows immediately from general properties of conditional probabilities. This was pointed out by S. Chapman | + | that is, a condition imposed on the [[Transition function|transition function]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/k/k055/k055680/k0556802.png" /> (<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/k/k055/k055680/k0556803.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/k/k055/k055680/k0556804.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/k/k055/k055680/k0556805.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/k/k055/k055680/k0556806.png" /> being a measurable space), enabling one (under certain conditions on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/k/k055/k055680/k0556807.png" />) to construct a [[Markov process|Markov process]] for which the conditional probability <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/k/k055/k055680/k0556808.png" /> is the same as <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/k/k055/k055680/k0556809.png" />. Conversely, for a Markov process its transition function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/k/k055/k055680/k05568010.png" />, which by definition is equal to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/k/k055/k055680/k05568011.png" />, satisfies the Kolmogorov–Chapman equation, as follows immediately from general properties of conditional probabilities. This was pointed out by S. Chapman {{Cite|C}} and investigated by A.N. Kolmogorov in 1931 (see {{Cite|K}}). |
====References==== | ====References==== | ||
| − | + | {| | |
| − | + | |valign="top"|{{Ref|C}}|| S. Chapman, "?", ''Proc. Roy. Soc. Ser. A'' , '''119''' (1928) pp. 34–54 | |
| − | + | |- | |
| + | |valign="top"|{{Ref|K}}|| A. Kolmogoroff, "Ueber die analytischen Methoden in der Wahrscheinlichkeitsrechnung" ''Math. Ann.'' , '''104''' (1931) pp. 415–458 | ||
| + | |- | ||
| + | |valign="top"|{{Ref|GS}}|| I.I. Gihman, A.V. Skorohod, "The theory of stochastic processes" , '''2''' , Springer (1975) (Translated from Russian) | ||
| + | |} | ||
====Comments==== | ====Comments==== | ||
| Line 20: | Line 24: | ||
====References==== | ====References==== | ||
| − | + | {| | |
| + | |valign="top"|{{Ref|L}}|| P. Lévy, "Processus stochastiques et mouvement Brownien", Gauthier-Villars (1965) | ||
| + | |- | ||
| + | |valign="top"|{{Ref|D}}|| E.B. Dynkin, "Markov processes", '''1''', Springer (1965) pp. Sect. 5.26 (Translated from Russian) | ||
| + | |- | ||
| + | |valign="top"|{{Ref|F}}|| W. Feller, [[Feller, "An introduction to probability theory and its applications"|"An introduction to probability theory and its applications"]], '''1''', Wiley (1966) pp. Chapt. XV.13 | ||
| + | |} | ||
Revision as of 11:35, 13 May 2012
2020 Mathematics Subject Classification: Primary: 60J35 [MSN][ZBL]
An equation of the form
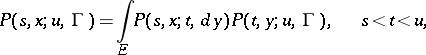 |
that is, a condition imposed on the transition function 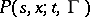 (
( ,
,  ,
, 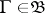 ,
, 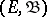 being a measurable space), enabling one (under certain conditions on
being a measurable space), enabling one (under certain conditions on 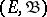 ) to construct a Markov process for which the conditional probability
) to construct a Markov process for which the conditional probability  is the same as
is the same as 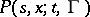 . Conversely, for a Markov process its transition function
. Conversely, for a Markov process its transition function 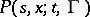 , which by definition is equal to
, which by definition is equal to 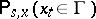 , satisfies the Kolmogorov–Chapman equation, as follows immediately from general properties of conditional probabilities. This was pointed out by S. Chapman [C] and investigated by A.N. Kolmogorov in 1931 (see [K]).
, satisfies the Kolmogorov–Chapman equation, as follows immediately from general properties of conditional probabilities. This was pointed out by S. Chapman [C] and investigated by A.N. Kolmogorov in 1931 (see [K]).
References
| [C] | S. Chapman, "?", Proc. Roy. Soc. Ser. A , 119 (1928) pp. 34–54 |
| [K] | A. Kolmogoroff, "Ueber die analytischen Methoden in der Wahrscheinlichkeitsrechnung" Math. Ann. , 104 (1931) pp. 415–458 |
| [GS] | I.I. Gihman, A.V. Skorohod, "The theory of stochastic processes" , 2 , Springer (1975) (Translated from Russian) |
Comments
In Western literature this equation is usually referred to as the Chapman–Kolmogorov equation.
See also (the editorial comments to) Einstein–Smoluchowski equation.
References
| [L] | P. Lévy, "Processus stochastiques et mouvement Brownien", Gauthier-Villars (1965) |
| [D] | E.B. Dynkin, "Markov processes", 1, Springer (1965) pp. Sect. 5.26 (Translated from Russian) |
| [F] | W. Feller, "An introduction to probability theory and its applications", 1, Wiley (1966) pp. Chapt. XV.13 |
Kolmogorov-Chapman equation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Kolmogorov-Chapman_equation&oldid=25929