Difference between revisions of "Branching process, age-dependent"
(→References: Mode: correct Zbl) |
(refs format) |
||
| Line 25: | Line 25: | ||
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b017/b017540/b01754019.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b017/b017540/b01754019.png" /></td> </tr></table> | ||
| − | The following results have been obtained for these processes | + | The following results have been obtained for these processes {{Cite|S}}: asymptotic formulas for the moments <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b017/b017540/b01754020.png" />, necessary and sufficient conditions of extinction, conditions of existence and uniqueness of a solution of equation (*) and asymptotic formulas as <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b017/b017540/b01754021.png" /> for |
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b017/b017540/b01754022.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b017/b017540/b01754022.png" /></td> </tr></table> | ||
| Line 35: | Line 35: | ||
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b017/b017540/b01754025.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b017/b017540/b01754025.png" /></td> </tr></table> | ||
| − | If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b017/b017540/b01754026.png" /> is independent of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b017/b017540/b01754027.png" />, the age-dependent branching process is a [[Bellman–Harris process|Bellman–Harris process]]. The model just described has been generalized to include processes with several types of particles, and also to processes for which a particle may generate new particles several times during its lifetime | + | If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b017/b017540/b01754026.png" /> is independent of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b017/b017540/b01754027.png" />, the age-dependent branching process is a [[Bellman–Harris process|Bellman–Harris process]]. The model just described has been generalized to include processes with several types of particles, and also to processes for which a particle may generate new particles several times during its lifetime {{Cite|S2}}, {{Cite|M}}. |
====References==== | ====References==== | ||
| − | + | {| | |
| − | + | |valign="top"|{{Ref|S}}|| B.A. Sewastjanow, "Verzweigungsprozesse" , Akad. Wissenschaft. DDR (1974) (Translated from Russian) {{MR|0408018}} {{ZBL|0291.60039}} | |
| − | + | |- | |
| + | |valign="top"|{{Ref|S2}}|| B.A. Sewastjanow, "Age-dependent branching processes" ''Theory Probab. Appl.'' , '''9''' : 4 (1964) pp. 521–537 ''Teor. Veroyatnost. i Primenen.'' , '''9''' : 4 (1964) pp. 577–594 {{MR|0170396}} {{ZBL|0248.60059}} | ||
| + | |- | ||
| + | |valign="top"|{{Ref|M}}|| C.J. Mode, "Multitype branching processes" , Elsevier (1971) {{MR|0279901}} {{ZBL|0219.60061}} | ||
| + | |} | ||
====Comments==== | ====Comments==== | ||
Additional references can be found in the article [[Branching process|Branching process]]. | Additional references can be found in the article [[Branching process|Branching process]]. | ||
Revision as of 06:17, 11 May 2012
2020 Mathematics Subject Classification: Primary: 60J80 [MSN][ZBL]
A model of a branching process in which the lifetime of a particle is an arbitrary non-negative random variable, while the number of daughter particles depends on its age at the moment of transformation. In the single-type particle model each particle has a random duration of life  with distribution function
with distribution function
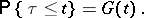 |
At the end of its life the particle is transformed into  daughter particles of age zero with a probability
daughter particles of age zero with a probability  if the transformation took place when the age attained by the original particle was
if the transformation took place when the age attained by the original particle was  . Let
. Let  be the number of particles at the moment of time
be the number of particles at the moment of time  . The generating function
. The generating function  of the probability distribution of
of the probability distribution of  for a process beginning with one particle of age zero satisfies the equation
for a process beginning with one particle of age zero satisfies the equation
 | (*) |
where
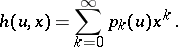 |
Put
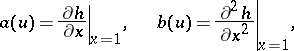 |
 |
An age-dependent branching process is said to be subcritical, critical or supercritical if 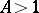 ,
, 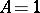 and
and 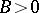 , or
, or 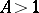 , respectively. The behaviour of the process as
, respectively. The behaviour of the process as 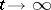 substantially depends on its criticality. Subcritical and critical processes die out with probability one, i.e.
substantially depends on its criticality. Subcritical and critical processes die out with probability one, i.e.
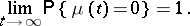 |
The following results have been obtained for these processes [S]: asymptotic formulas for the moments 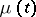 , necessary and sufficient conditions of extinction, conditions of existence and uniqueness of a solution of equation (*) and asymptotic formulas as
, necessary and sufficient conditions of extinction, conditions of existence and uniqueness of a solution of equation (*) and asymptotic formulas as 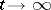 for
for
 |
The limit distributions have also been determined. In the critical case, as  :
:
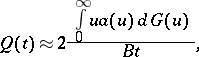 |
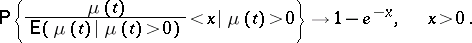 |
If 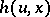 is independent of
is independent of  , the age-dependent branching process is a Bellman–Harris process. The model just described has been generalized to include processes with several types of particles, and also to processes for which a particle may generate new particles several times during its lifetime [S2], [M].
, the age-dependent branching process is a Bellman–Harris process. The model just described has been generalized to include processes with several types of particles, and also to processes for which a particle may generate new particles several times during its lifetime [S2], [M].
References
| [S] | B.A. Sewastjanow, "Verzweigungsprozesse" , Akad. Wissenschaft. DDR (1974) (Translated from Russian) MR0408018 Zbl 0291.60039 |
| [S2] | B.A. Sewastjanow, "Age-dependent branching processes" Theory Probab. Appl. , 9 : 4 (1964) pp. 521–537 Teor. Veroyatnost. i Primenen. , 9 : 4 (1964) pp. 577–594 MR0170396 Zbl 0248.60059 |
| [M] | C.J. Mode, "Multitype branching processes" , Elsevier (1971) MR0279901 Zbl 0219.60061 |
Comments
Additional references can be found in the article Branching process.
Branching process, age-dependent. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Branching_process,_age-dependent&oldid=25672