Difference between revisions of "Binomial distribution"
(→References: Gnedenko: closest MR, Zbl; Feller: internal link) |
(→References: Prokhorov: MR) |
||
| Line 62: | Line 62: | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> B.V. Gnedenko, "The theory of probability", Chelsea, reprint (1962) (Translated from Russian) {{MR|0217823}} {{MR|0217824}} {{ZBL|0191.46702}} </TD></TR> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> B.V. Gnedenko, "The theory of probability", Chelsea, reprint (1962) (Translated from Russian) {{MR|0217823}} {{MR|0217824}} {{ZBL|0191.46702}} </TD></TR> | ||
<TR><TD valign="top">[2]</TD> <TD valign="top"> W. Feller, [[Feller, "An introduction to probability theory and its applications"|"An introduction to probability theory and its applications"]], Wiley (1957–1971)</TD></TR> | <TR><TD valign="top">[2]</TD> <TD valign="top"> W. Feller, [[Feller, "An introduction to probability theory and its applications"|"An introduction to probability theory and its applications"]], Wiley (1957–1971)</TD></TR> | ||
| − | <TR><TD valign="top">[3]</TD> <TD valign="top"> Yu.V. [Yu.V. Prokhorov] Prohorov, Yu.A. Rozanov, "Probability theory, basic concepts. Limit theorems, random processes" , Springer (1969) (Translated from Russian) {{MR|0251754}} {{ZBL|}} </TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> Yu.V. Prokhorov, "Asymptotic behaviour of the binomial distribution" ''Selected Translations in Math. Stat. and Probab.'' , '''1''' , Amer. Math. Soc. (1961) (Translated from Russian) ''Uspekhi Mat. Nauk'' , '''8''' : 3 (1953) pp. 135–142</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> L.N. Bol'shev, N.V. Smirnov, "Tables of mathematical statistics" , ''Libr. math. tables'' , '''46''' , Nauka (1983) (In Russian) (Processed by L.S. Bark and E.S. Kedrova) {{MR|}} {{ZBL|0529.62099}} </TD></TR></table> | + | <TR><TD valign="top">[3]</TD> <TD valign="top"> Yu.V. [Yu.V. Prokhorov] Prohorov, Yu.A. Rozanov, "Probability theory, basic concepts. Limit theorems, random processes" , Springer (1969) (Translated from Russian) {{MR|0251754}} {{ZBL|}} </TD></TR> |
| + | <TR><TD valign="top">[4]</TD> <TD valign="top"> Yu.V. Prokhorov, "Asymptotic behaviour of the binomial distribution" ''Selected Translations in Math. Stat. and Probab.'' , '''1''' , Amer. Math. Soc. (1961) {{MR|0116370}} (Translated from Russian) ''Uspekhi Mat. Nauk'' , '''8''' : 3 (1953) pp. 135–142 {{MR|0056861}} </TD></TR> | ||
| + | <TR><TD valign="top">[5]</TD> <TD valign="top"> L.N. Bol'shev, N.V. Smirnov, "Tables of mathematical statistics" , ''Libr. math. tables'' , '''46''' , Nauka (1983) (In Russian) (Processed by L.S. Bark and E.S. Kedrova) {{MR|}} {{ZBL|0529.62099}} </TD></TR></table> | ||
Revision as of 11:20, 1 April 2012
Bernoulli distribution
2020 Mathematics Subject Classification: Primary: 60E99 [MSN][ZBL]
The probability distribution of a random variable  which assumes integral values
which assumes integral values  with the probabilities
with the probabilities
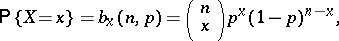 |
where  is the binomial coefficient, and
is the binomial coefficient, and  is a parameter of the binomial distribution, called the probability of a positive outcome, which can take values in the interval
is a parameter of the binomial distribution, called the probability of a positive outcome, which can take values in the interval  . The binomial distribution is one of the fundamental probability distributions connected with a sequence of independent trials. Let
. The binomial distribution is one of the fundamental probability distributions connected with a sequence of independent trials. Let  be a sequence of independent random variables, each one of which may assume only one of the values 1 and 0 with respective probabilities
be a sequence of independent random variables, each one of which may assume only one of the values 1 and 0 with respective probabilities  and
and  (i.e. all
(i.e. all 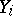 are binomially distributed with
are binomially distributed with 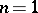 ). The values of
). The values of 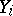 may be treated as the results of independent trials, with
may be treated as the results of independent trials, with 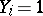 if the result of the
if the result of the 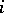 -th trial is "positive" and
-th trial is "positive" and  if it is "negative" . If the total number of independent trials
if it is "negative" . If the total number of independent trials  is fixed, such a scheme is known as Bernoulli trials, and the total number of positive results,
is fixed, such a scheme is known as Bernoulli trials, and the total number of positive results,
 |
is then binomially distributed with parameter  .
.
The mathematical expectation  (the generating function of the binomial distribution) for any value of
(the generating function of the binomial distribution) for any value of  is the polynomial
is the polynomial 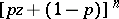 , the representation of which by Newton's binomial series has the form
, the representation of which by Newton's binomial series has the form
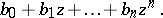 |
(Hence the very name "binomial distribution" .) The moments (cf. Moment) of a binomial distribution are given by the formulas
 |
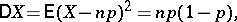 |
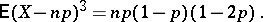 |
The binomial distribution function is defined, for any real 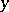 ,
, 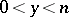 , by the formula
, by the formula
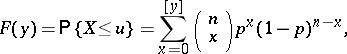 |
where  is the integer part of
is the integer part of 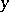 , and
, and
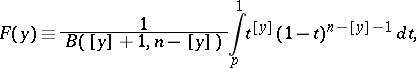 |
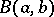 is Euler's beta-function, and the integral on the right-hand side is known as the incomplete beta-function.
is Euler's beta-function, and the integral on the right-hand side is known as the incomplete beta-function.
As  , the binomial distribution function is expressed in terms of the standard normal distribution function
, the binomial distribution function is expressed in terms of the standard normal distribution function  by the asymptotic formula (the de Moivre–Laplace theorem):
by the asymptotic formula (the de Moivre–Laplace theorem):
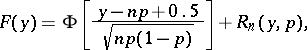 |
where
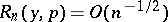 |
uniformly for all real 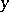 . There also exist other, higher order, normal approximations of the binomial distribution.
. There also exist other, higher order, normal approximations of the binomial distribution.
If the number of independent trials  is large, while the probability
is large, while the probability 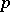 is small, the individual probabilities
is small, the individual probabilities 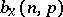 can be approximately expressed in terms of the Poisson distribution:
can be approximately expressed in terms of the Poisson distribution:
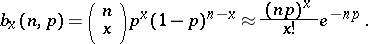 |
If 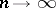 and
and 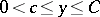 (where
(where  and
and  are constants), the asymptotic formula
are constants), the asymptotic formula
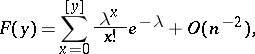 |
where 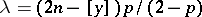 , is uniformly valid with respect to all
, is uniformly valid with respect to all  in the interval
in the interval 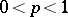 .
.
The multinomial distribution is the multi-dimensional generalization of the binomial distribution.
References
| [1] | B.V. Gnedenko, "The theory of probability", Chelsea, reprint (1962) (Translated from Russian) MR0217823 MR0217824 Zbl 0191.46702 |
| [2] | W. Feller, "An introduction to probability theory and its applications", Wiley (1957–1971) |
| [3] | Yu.V. [Yu.V. Prokhorov] Prohorov, Yu.A. Rozanov, "Probability theory, basic concepts. Limit theorems, random processes" , Springer (1969) (Translated from Russian) MR0251754 |
| [4] | Yu.V. Prokhorov, "Asymptotic behaviour of the binomial distribution" Selected Translations in Math. Stat. and Probab. , 1 , Amer. Math. Soc. (1961) MR0116370 (Translated from Russian) Uspekhi Mat. Nauk , 8 : 3 (1953) pp. 135–142 MR0056861 |
| [5] | L.N. Bol'shev, N.V. Smirnov, "Tables of mathematical statistics" , Libr. math. tables , 46 , Nauka (1983) (In Russian) (Processed by L.S. Bark and E.S. Kedrova) Zbl 0529.62099 |
Binomial distribution. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Binomial_distribution&oldid=24175