Difference between revisions of "Affine scheme"
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
m |
||
| Line 1: | Line 1: | ||
| − | A generalization of the concept of an [[Affine variety|affine variety]], which plays the role of a local object in the theory of schemes. Let | + | A generalization of the concept of an [[Affine variety|affine variety]], which plays the role of a local object in the theory of schemes. Let $ A $ be a commutative ring with a unit. An affine scheme consists of a topological space $ \text{Spec}(A) $ and a sheaf of rings $ \widetilde{A} $ on $ \text{Spec}(A) $. Here, $ \text{Spec}(A) $ is the set of all prime ideals of $ A $ (called ‘the points of the affine scheme’) equipped with the [[Zariski topology|Zariski topology]] (or equivalently with the spectral topology), in which a basis of open sets is given by $ D(f) = \{ \mathfrak{p} \in \text{Spec}(A) \mid f \notin \mathfrak{p} \} $, where $ f $ runs through the elements of $ A $. The sheaf $ \widetilde{A} $ of local rings is defined by the condition that $ \Gamma \left( D(f),\tilde{A} \right) = A_{f} $, where $ A_{f} $ is the localization of the ring $ A $ with respect to the multiplicative system $ \{ f^{n} \}_{n \in \Bbb{N}_{0}} $ (cf. [[Localization in a commutative algebra|Localization in a commutative algebra]]). |
Affine schemes were first introduced by A. Grothendieck [[#References|[1]]], who created the theory of schemes. A scheme is a ringed space which is locally isomorphic to an affine scheme. | Affine schemes were first introduced by A. Grothendieck [[#References|[1]]], who created the theory of schemes. A scheme is a ringed space which is locally isomorphic to an affine scheme. | ||
| − | An affine scheme | + | An affine scheme $ \text{Spec}(A) $ is called ‘Noetherian’ (‘integral’, ‘reduced’, ‘normal’, or ‘regular’, respectively) if the ring $ A $ is Noetherian (integral, without nilpotents, integrally closed, or regular, respectively). An affine scheme is called connected (irreducible, discrete, or quasi-compact, respectively) if the topological space $ \text{Spec}(A) $ also has these properties. The space $ \text{Spec}(A) $ of an affine scheme is always compact (and usually not Hausdorff). |
| − | The affine schemes form a category if the morphisms of these schemes, considered as locally ringed spaces, are considered as morphisms of affine schemes. Each homomorphism of rings | + | The affine schemes form a category if the morphisms of these schemes, considered as locally ringed spaces, are considered as morphisms of affine schemes. Each homomorphism of rings $ \phi: A \to B $ defines a morphism of affine schemes: $ \left( \text{Spec}(B),\widetilde{B} \right) \to \left( \text{Spec}(A),\widetilde{A} \right) $, consisting of the continuous mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a011/a011090/a01109021.png" /> (<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a011/a011090/a01109022.png" /> for $ \mathfrak{p} \in \text{Spec}(B) $), and a homomorphism of sheaves of rings <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a011/a011090/a01109024.png" />, which transforms the section $ a / f $ of the sheaf $ \widetilde{A} $ over the set $ D(f) $ into the section $ \phi(a) / \phi(f) $. The morphisms of an arbitrary scheme $ (X,\mathcal{O}_{X}) $ into an affine scheme $ \left( \text{Spec}(A),\widetilde{A} \right) $ (which are also called ‘$ X $-valued points of $ \text{Spec}(A) $’) are in a one-to-one correspondence with the homomorphisms of rings $ A \to \Gamma(X,\mathcal{O}_{X}) $; thus, the correspondence $ A \mapsto \left( \text{Spec}(A),\widetilde{A} \right) $ is a contravariant functor from the category of commutative rings with a unit into the category of affine schemes, which establishes an anti-equivalence of these categories. In particular, in the category of affine schemes there are finite direct sums and fibre products, dual to the constructions of the direct sum and the tensor product of rings. The morphisms of affine schemes which correspond to surjective homomorphisms of rings are called closed imbeddings of affine schemes. |
The most important examples of affine schemes are affine varieties; other examples are affine group schemes (cf. [[Group scheme|Group scheme]]). | The most important examples of affine schemes are affine varieties; other examples are affine group schemes (cf. [[Group scheme|Group scheme]]). | ||
| − | In a manner similar to the construction of the sheaf | + | In a manner similar to the construction of the sheaf $ \widetilde{A} $, it is possible to construct, for any $ A $-module $ M $, a sheaf $ \widetilde{M} $ of $ \widetilde{A} $-modules on $ \text{Spec}(A) $ for which |
| − | + | $$ | |
| − | + | \Gamma \left( D(f),\widetilde{M} \right) = M_{f} = M \otimes_{A} A_{f}. | |
| − | + | $$ | |
| − | Such sheaves are called quasi-coherent. The category of | + | Such sheaves are called quasi-coherent. The category of $ A $-modules is equivalent to the category of quasi-coherent sheaves of $ \widetilde{A} $-modules on $ \text{Spec}(A) $; projective modules correspond to locally free sheaves. The cohomology spaces of quasi-coherent sheaves over an affine scheme are described by Serre’s theorem: |
| − | + | $$ | |
| − | + | H^{q} \left( \text{Spec}(A),\widetilde{M} \right) = 0 \quad \text{if $ q > 0 $}. | |
| − | + | $$ | |
| − | The converse of this theorem ( | + | The converse of this theorem (Serre’s criterion for affinity) states that if $ (X,\mathcal{O}_{X}) $ is a compact separable scheme, and if $ {H^{1}}(X,F) = 0 $ for any quasi-coherent sheaf $ F $ of $ \mathcal{O}_{X} $-modules, then $ X $ is an affine scheme. Other criteria for affinity also exist [[#References|[1]]], [[#References|[4]]]. |
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> A. Grothendieck, J. Dieudonné, | + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> A. Grothendieck, J. Dieudonné, “Eléments de géometrie algébrique”, ''Publ. Math. IHES'', '''4''' (1960). {{MR|0217083}} {{MR|0163908}} {{ZBL|0118.36206}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> J. Dieudonné, “Algebraic geometry”, ''Adv. in Math.'', '''1''' (1969), pp. 233–321. {{MR|0244267}} {{ZBL|0185.49102}} </TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> Yu.I. Manin, “Lectures on algebraic geometry”, '''1''', Moscow (1970) (In Russian). {{MR|0284434}} {{ZBL|0204.21302}} </TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> J. Goodman, R. Hartshorne, “Schemes with finite-dimensional cohomology groups”, ''Amer. J. Math.'', '''91''' (1969), pp. 258–266. {{MR|0241432}} {{ZBL|0176.18303}} </TD></TR></table> |
| − | |||
| − | |||
====Comments==== | ====Comments==== | ||
| Line 28: | Line 26: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> R. Hartshorne, | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> R. Hartshorne, “Algebraic geometry”, Springer (1977). {{MR|0463157}} {{ZBL|0367.14001}} </TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> A. Grothendieck, J. Dieudonné, “Eléments de géometrie algébrique”, '''I. Le langage des schémes''', Springer (1971). {{MR|0217085}} {ZBL|0203.23301}} </TD></TR></table> |
Revision as of 07:14, 2 September 2015
A generalization of the concept of an affine variety, which plays the role of a local object in the theory of schemes. Let $ A $ be a commutative ring with a unit. An affine scheme consists of a topological space $ \text{Spec}(A) $ and a sheaf of rings $ \widetilde{A} $ on $ \text{Spec}(A) $. Here, $ \text{Spec}(A) $ is the set of all prime ideals of $ A $ (called ‘the points of the affine scheme’) equipped with the Zariski topology (or equivalently with the spectral topology), in which a basis of open sets is given by $ D(f) = \{ \mathfrak{p} \in \text{Spec}(A) \mid f \notin \mathfrak{p} \} $, where $ f $ runs through the elements of $ A $. The sheaf $ \widetilde{A} $ of local rings is defined by the condition that $ \Gamma \left( D(f),\tilde{A} \right) = A_{f} $, where $ A_{f} $ is the localization of the ring $ A $ with respect to the multiplicative system $ \{ f^{n} \}_{n \in \Bbb{N}_{0}} $ (cf. Localization in a commutative algebra).
Affine schemes were first introduced by A. Grothendieck [1], who created the theory of schemes. A scheme is a ringed space which is locally isomorphic to an affine scheme.
An affine scheme $ \text{Spec}(A) $ is called ‘Noetherian’ (‘integral’, ‘reduced’, ‘normal’, or ‘regular’, respectively) if the ring $ A $ is Noetherian (integral, without nilpotents, integrally closed, or regular, respectively). An affine scheme is called connected (irreducible, discrete, or quasi-compact, respectively) if the topological space $ \text{Spec}(A) $ also has these properties. The space $ \text{Spec}(A) $ of an affine scheme is always compact (and usually not Hausdorff).
The affine schemes form a category if the morphisms of these schemes, considered as locally ringed spaces, are considered as morphisms of affine schemes. Each homomorphism of rings $ \phi: A \to B $ defines a morphism of affine schemes: $ \left( \text{Spec}(B),\widetilde{B} \right) \to \left( \text{Spec}(A),\widetilde{A} \right) $, consisting of the continuous mapping 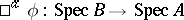 (
(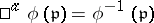 for $ \mathfrak{p} \in \text{Spec}(B) $), and a homomorphism of sheaves of rings
for $ \mathfrak{p} \in \text{Spec}(B) $), and a homomorphism of sheaves of rings 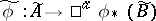 , which transforms the section $ a / f $ of the sheaf $ \widetilde{A} $ over the set $ D(f) $ into the section $ \phi(a) / \phi(f) $. The morphisms of an arbitrary scheme $ (X,\mathcal{O}_{X}) $ into an affine scheme $ \left( \text{Spec}(A),\widetilde{A} \right) $ (which are also called ‘$ X $-valued points of $ \text{Spec}(A) $’) are in a one-to-one correspondence with the homomorphisms of rings $ A \to \Gamma(X,\mathcal{O}_{X}) $; thus, the correspondence $ A \mapsto \left( \text{Spec}(A),\widetilde{A} \right) $ is a contravariant functor from the category of commutative rings with a unit into the category of affine schemes, which establishes an anti-equivalence of these categories. In particular, in the category of affine schemes there are finite direct sums and fibre products, dual to the constructions of the direct sum and the tensor product of rings. The morphisms of affine schemes which correspond to surjective homomorphisms of rings are called closed imbeddings of affine schemes.
, which transforms the section $ a / f $ of the sheaf $ \widetilde{A} $ over the set $ D(f) $ into the section $ \phi(a) / \phi(f) $. The morphisms of an arbitrary scheme $ (X,\mathcal{O}_{X}) $ into an affine scheme $ \left( \text{Spec}(A),\widetilde{A} \right) $ (which are also called ‘$ X $-valued points of $ \text{Spec}(A) $’) are in a one-to-one correspondence with the homomorphisms of rings $ A \to \Gamma(X,\mathcal{O}_{X}) $; thus, the correspondence $ A \mapsto \left( \text{Spec}(A),\widetilde{A} \right) $ is a contravariant functor from the category of commutative rings with a unit into the category of affine schemes, which establishes an anti-equivalence of these categories. In particular, in the category of affine schemes there are finite direct sums and fibre products, dual to the constructions of the direct sum and the tensor product of rings. The morphisms of affine schemes which correspond to surjective homomorphisms of rings are called closed imbeddings of affine schemes.
The most important examples of affine schemes are affine varieties; other examples are affine group schemes (cf. Group scheme).
In a manner similar to the construction of the sheaf $ \widetilde{A} $, it is possible to construct, for any $ A $-module $ M $, a sheaf $ \widetilde{M} $ of $ \widetilde{A} $-modules on $ \text{Spec}(A) $ for which $$ \Gamma \left( D(f),\widetilde{M} \right) = M_{f} = M \otimes_{A} A_{f}. $$ Such sheaves are called quasi-coherent. The category of $ A $-modules is equivalent to the category of quasi-coherent sheaves of $ \widetilde{A} $-modules on $ \text{Spec}(A) $; projective modules correspond to locally free sheaves. The cohomology spaces of quasi-coherent sheaves over an affine scheme are described by Serre’s theorem: $$ H^{q} \left( \text{Spec}(A),\widetilde{M} \right) = 0 \quad \text{if $ q > 0 $}. $$ The converse of this theorem (Serre’s criterion for affinity) states that if $ (X,\mathcal{O}_{X}) $ is a compact separable scheme, and if $ {H^{1}}(X,F) = 0 $ for any quasi-coherent sheaf $ F $ of $ \mathcal{O}_{X} $-modules, then $ X $ is an affine scheme. Other criteria for affinity also exist [1], [4].
References
| [1] | A. Grothendieck, J. Dieudonné, “Eléments de géometrie algébrique”, Publ. Math. IHES, 4 (1960). MR0217083 MR0163908 Zbl 0118.36206 |
| [2] | J. Dieudonné, “Algebraic geometry”, Adv. in Math., 1 (1969), pp. 233–321. MR0244267 Zbl 0185.49102 |
| [3] | Yu.I. Manin, “Lectures on algebraic geometry”, 1, Moscow (1970) (In Russian). MR0284434 Zbl 0204.21302 |
| [4] | J. Goodman, R. Hartshorne, “Schemes with finite-dimensional cohomology groups”, Amer. J. Math., 91 (1969), pp. 258–266. MR0241432 Zbl 0176.18303 |
Comments
Reference [a1] is, of course, standard. It replaces [3]. An alternative to [1] is [a2].
References
| [a1] | R. Hartshorne, “Algebraic geometry”, Springer (1977). MR0463157 Zbl 0367.14001 |
| [a2] | A. Grothendieck, J. Dieudonné, “Eléments de géometrie algébrique”, I. Le langage des schémes, Springer (1971). MR0217085 {ZBL|0203.23301}} |
Affine scheme. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Affine_scheme&oldid=23741