Markov chain, recurrent

2020 Mathematics Subject Classification: Primary: 60J10 [MSN][ZBL]

A Markov chain in which a random trajectory 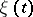, starting at any state 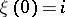, returns to that state with probability 1. In terms of the transition probabilities 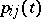, recurrence of a discrete-time Markov chain is equivalent to the divergence for any 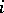of the series

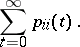In a recurrent Markov chain a trajectory 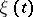, , , returns infinitely often to the state 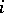with probability 1. In a recurrent Markov chain there are no inessential states and the essential states decompose into recurrent classes. An example of a recurrent Markov chain is the symmetric random walk on the integer lattice on the line or plane. In the symmetric walk on the line a particle moves from position to 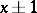with probabilities 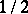; in the symmetric walk on the plane a particle moves from 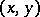to one of the four points 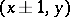, 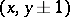with probabilities 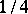. In these examples a particle, starting the walk at an arbitrary point, returns to that point with probability 1. The symmetric walk on the integer lattice in the three-dimensional space, when the probability of transition from to a neighbouring point 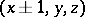, , 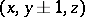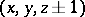is equal to 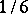, is not recurrent. In this case the probability of return of the particle to its initial point is approximately 0.35.

References

[1]	W. Feller, "An introduction to probability theory and its applications", 1 , Wiley (1966)

References

[a1]	D. Freeman, "Markov chains" , Holden-Day (1975)
[a2]	M. Iosifescu, "Finite Markov processes and their applications" , Wiley (1980) MR0587116 Zbl 0436.60001
[a3]	J.G. Kemeny, J.L. Snell, "Finite Markov chains" , v. Nostrand (1960) MR1531032 MR0115196 Zbl 0089.13704
[a4]	J.G. Kemeny, J.L. Snell, A.W. Knapp, "Denumerable Markov chains" , Springer (1976) MR0407981 Zbl 0348.60090
[a5]	D. Revuz, "Markov chains" , North-Holland (1975) MR0415773 Zbl 0332.60045
[a6]	V.I. [V.I. Romanovskii] Romanovsky, "Discrete Markov chains" , Wolters-Noordhoff (1970) (Translated from Russian) MR0266312 Zbl 0201.20002
[a7]	E. Seneta, "Non-negative matrices and Markov chains" , Springer (1981) MR2209438 Zbl 0471.60001
[a8]	V. Spitzer, "Principles of random walk" , v. Nostrand (1964) MR0171290 Zbl 0119.34304