Difference between revisions of "Borel strong law of large numbers"
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
(refs format) |
||
| Line 3: | Line 3: | ||
[[Category:Limit theorems]] | [[Category:Limit theorems]] | ||
| − | Historically, the first variant of the [[Strong law of large numbers|strong law of large numbers]], formulated and proved by E. Borel | + | Historically, the first variant of the [[Strong law of large numbers|strong law of large numbers]], formulated and proved by E. Borel {{Cite|B}} in the context of the Bernoulli scheme (cf. [[Bernoulli trials|Bernoulli trials]]). Consider independent random variables <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b017/b017150/b0171501.png" /> which are identically distributed and assume one of two values 0 and 1 with probability of 1/2 each; the expression <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b017/b017150/b0171502.png" /> will then give the number of successful trials in a Bernoulli scheme in which the probability of success is 1/2. Borel {{Cite|B}} showed that |
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b017/b017150/b0171503.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b017/b017150/b0171503.png" /></td> </tr></table> | ||
| Line 18: | Line 18: | ||
====References==== | ====References==== | ||
| − | + | {| | |
| + | |valign="top"|{{Ref|B}}|| E. Borel, "Les probabilités dénombrables et leurs applications arithmetique" ''Rend. Circ. Mat. Palermo (2)'' , '''27''' (1909) pp. 247–271 | ||
| + | |- | ||
| + | |valign="top"|{{Ref|K}}|| M. Kac, "Statistical independence in probability, analysis and number theory" , Math. Assoc. Amer. (1963) {{MR|1530983}} {{MR|0110114}} {{ZBL|0112.09101}} | ||
| + | |} | ||
Revision as of 06:10, 11 May 2012
2020 Mathematics Subject Classification: Primary: 60F15 [MSN][ZBL]
Historically, the first variant of the strong law of large numbers, formulated and proved by E. Borel [B] in the context of the Bernoulli scheme (cf. Bernoulli trials). Consider independent random variables 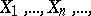 which are identically distributed and assume one of two values 0 and 1 with probability of 1/2 each; the expression
which are identically distributed and assume one of two values 0 and 1 with probability of 1/2 each; the expression 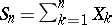 will then give the number of successful trials in a Bernoulli scheme in which the probability of success is 1/2. Borel [B] showed that
will then give the number of successful trials in a Bernoulli scheme in which the probability of success is 1/2. Borel [B] showed that
 |
with probability one as 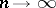 . It was subsequently (1914) shown by G.H. Hardy and J.E. Littlewood that, almost certainly,
. It was subsequently (1914) shown by G.H. Hardy and J.E. Littlewood that, almost certainly,
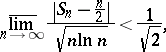 |
after which (1922) the stronger result:
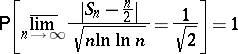 |
was proved by A.Ya. Khinchin. See also Law of the iterated logarithm.
References
| [B] | E. Borel, "Les probabilités dénombrables et leurs applications arithmetique" Rend. Circ. Mat. Palermo (2) , 27 (1909) pp. 247–271 |
| [K] | M. Kac, "Statistical independence in probability, analysis and number theory" , Math. Assoc. Amer. (1963) MR1530983 MR0110114 Zbl 0112.09101 |
Borel strong law of large numbers. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Borel_strong_law_of_large_numbers&oldid=23584