Difference between revisions of "Baire set"
From Encyclopedia of Mathematics
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
(refs format) |
||
| Line 8: | Line 8: | ||
====References==== | ====References==== | ||
| − | + | {| | |
| + | |valign="top"|{{Ref|H}}|| P.R. Halmos, "Measure theory" , v. Nostrand (1950) {{MR|0033869}} {{ZBL|0040.16802}} | ||
| + | |} | ||
Revision as of 19:57, 10 May 2012
in a locally compact Hausdorff space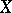 
2020 Mathematics Subject Classification: Primary: 28A05 Secondary: 03E1554H05 [MSN][ZBL]
A set belonging to the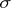 
-ring generated by the class of all compact sets in 
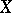that are 
-sets. A Baire set serves to define the concept of a Baire-measurable function. In all classical particular cases in which measure theory is developed in topological spaces, e.g. in Euclidean spaces, the concept of a Baire set coincides with that of a Borel set.
References
| [H] | P.R. Halmos, "Measure theory" , v. Nostrand (1950) MR0033869 Zbl 0040.16802 |
How to Cite This Entry:
Baire set. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Baire_set&oldid=23578
Baire set. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Baire_set&oldid=23578
This article was adapted from an original article by V.A. Skvortsov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article