Difference between revisions of "Brøndsted-Rockafellar theorem"
Ulf Rehmann (talk | contribs) m (moved Brondsted-Rockafellar theorem to Brøndsted-Rockafellar theorem: accented title) |
m (link) |
||
| Line 1: | Line 1: | ||
| − | An extended-real-valued function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110920/b1109201.png" /> on a [[Banach space|Banach space]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110920/b1109202.png" /> over the real numbers <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110920/b1109203.png" /> is said to be proper if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110920/b1109204.png" /> for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110920/b1109205.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110920/b1109206.png" /> for at least one point <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110920/b1109207.png" />. The epigraph of such a function is the subset of the product space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110920/b1109208.png" /> defined by | + | An extended-real-valued function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110920/b1109201.png" /> on a [[Banach space|Banach space]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110920/b1109202.png" /> over the real numbers <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110920/b1109203.png" /> is said to be proper if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110920/b1109204.png" /> for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110920/b1109205.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110920/b1109206.png" /> for at least one point <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110920/b1109207.png" />. The [[epigraph]] of such a function is the subset of the product space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110920/b1109208.png" /> defined by |
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110920/b1109209.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110920/b1109209.png" /></td> </tr></table> | ||
Revision as of 17:02, 7 May 2017
An extended-real-valued function 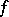 on a Banach space
on a Banach space 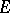 over the real numbers
over the real numbers 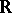 is said to be proper if
is said to be proper if  for all
for all 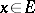 and
and  for at least one point
for at least one point  . The epigraph of such a function is the subset of the product space
. The epigraph of such a function is the subset of the product space  defined by
defined by
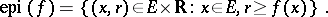 |
The function 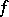 is convex (cf. Convex function (of a real variable)) precisely when the set
is convex (cf. Convex function (of a real variable)) precisely when the set  is convex (cf. Convex set) and
is convex (cf. Convex set) and  is lower semi-continuous (cf. Semi-continuous function) precisely when
is lower semi-continuous (cf. Semi-continuous function) precisely when 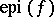 is closed (cf. Closed set). A continuous linear functional
is closed (cf. Closed set). A continuous linear functional 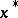 on
on  (that is, a member of the dual space
(that is, a member of the dual space  ) is said to be a subgradient of
) is said to be a subgradient of 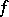 at the point
at the point  provided
provided  and
and 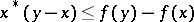 for all
for all 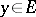 . The set of all subgradients to
. The set of all subgradients to 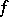 at
at  (where
(where 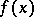 is finite) forms the subdifferential
is finite) forms the subdifferential 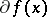 of
of 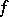 at
at  . The Brøndsted–Rockafellar theorem [a2] asserts that for a proper convex lower semi-continuous function
. The Brøndsted–Rockafellar theorem [a2] asserts that for a proper convex lower semi-continuous function 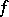 , the set of points where
, the set of points where 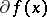 is non-empty is dense in the set of
is non-empty is dense in the set of  where
where 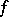 is finite (cf. Dense set). This is related to the Bishop–Phelps theorem [a1] (and the proof uses techniques of the latter), since a subgradient at a point
is finite (cf. Dense set). This is related to the Bishop–Phelps theorem [a1] (and the proof uses techniques of the latter), since a subgradient at a point  can be identified with a support functional (cf. Support function) of
can be identified with a support functional (cf. Support function) of 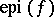 at the point
at the point  . These techniques were again applied to obtain minimization results (the Ekeland variational principle) for non-convex lower semi-continuous functions [a3]; see [a4] for a survey.
. These techniques were again applied to obtain minimization results (the Ekeland variational principle) for non-convex lower semi-continuous functions [a3]; see [a4] for a survey.
References
| [a1] | E. Bishop, R.R. Phelps, "The support functionals of a convex set" P. Klee (ed.) , Convexity , Proc. Symp. Pure Math. , 7 , Amer. Math. Soc. (1963) pp. 27–35 |
| [a2] | A. Brøndsted, R.T. Rockafellar, "On the subdifferentiability of convex functions" Proc. Amer. Math. Soc. , 16 (1965) pp. 605–611 |
| [a3] | I. Ekeland, "On the variational principle" J. Math. Anal. Appl. , 47 (1974) pp. 324–353 |
| [a4] | I. Ekeland, "Nonconvex minimization problems" Bull. Amer. Math. Soc. (NS) , 1 (1979) pp. 443–474 |
Brøndsted-Rockafellar theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Br%C3%B8ndsted-Rockafellar_theorem&oldid=23200