Fréchet differential

at a point 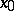of a mapping 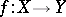of a normed space 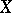into a normed space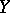

The mapping 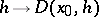which is linear and continuous from 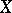into 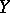and has the property that

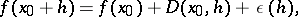(1)

where

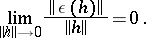If a mapping 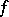admits an expansion (1) at a point 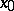, then it is said to be Fréchet differentiable, and the actual operator

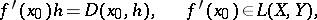is called the Fréchet derivative.

For a function 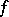in a finite number of variables, the Fréchet differential is the linear function

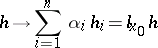that has the property that

(2)

where 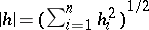or any other equivalent norm in . Here 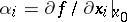are the partial derivatives of 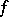at .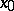

Definition (2), which is now commonplace, apparently first appeared in an explicit form in the lectures of K. Weierstrass (1861, see [1]). At the end of the 19th century this definition gradually came into the textbooks (see [2], [3] and others). But at the time when M. Fréchet began to develop infinite-dimensional analysis, the now classical definition of the differential was so far from commonplace that even Fréchet himself supposed that his definition of the differential in an infinite-dimensional space was a new concept in the finite-dimensional case too. Nowadays the term is only used in relation to infinite-dimensional mappings. See Gâteaux differential; Differential.

References

[1]	P. Dugac, "Eléments d'analyse de Karl Weierstrass" , Paris (1972)
[2]	O. Stolz, "Grundzüge der Differential- und Integralrechnung" , 1 , Teubner (1893)
[3]	W. Young, "The fundamental theorems of the differential calculus" , Cambridge Univ. Press (1910)
[4]	M. Fréchet, "Sur la notion de différentielle" C.R. Acad. Sci. Paris , 152 (1911) pp. 845–847; 1050–1051
[5]	M. Fréchet, "Sur la notion de différentielle totale" Nouvelles Ann. Math. Sér. 4 , 12 (1912) pp. 385–403; 433–449
[6]	A.N. Kolmogorov, S.V. Fomin, "Elements of the theory of functions and functional analysis" , 1–2 , Graylock (1957–1961) (Translated from Russian)
[7]	V.M. Alekseev, V.M. Tikhomirov, S.V. Fomin, "Optimal control" , Consultants Bureau (1987) (Translated from Russian)