Difference between revisions of "Brooks-Jewett theorem"
Ulf Rehmann (talk | contribs) m (moved Brooks–Jewett theorem to Brooks-Jewett theorem: ascii title) |
m (AUTOMATIC EDIT (latexlist): Replaced 55 formulas out of 57 by TEX code with an average confidence of 2.0 and a minimal confidence of 2.0.) |
||
| Line 1: | Line 1: | ||
| − | + | <!--This article has been texified automatically. Since there was no Nroff source code for this article, | |
| + | the semi-automatic procedure described at https://encyclopediaofmath.org/wiki/User:Maximilian_Janisch/latexlist | ||
| + | was used. | ||
| + | If the TeX and formula formatting is correct, please remove this message and the {{TEX|semi-auto}} category. | ||
| − | + | Out of 57 formulas, 55 were replaced by TEX code.--> | |
| − | + | {{TEX|semi-auto}}{{TEX|partial}} | |
| + | Let $X$ be a [[Topological group|topological group]]. A [[Set function|set function]] $m : \Sigma \rightarrow X$ is exhaustive (also called strongly bounded) if $\operatorname { lim } _ { n \rightarrow \infty } m ( E _ { n } ) = 0$ for each sequence $\{ E _ { n } \}$ of pairwise disjoint sets from the $\sigma$-algebra $\Sigma$ (cf. also [[Measure|Measure]]). A sequence $\{ m_i \}$ of set functions $m _ { i } : \Sigma \rightarrow X$, $i \in \mathbf{N}$, is uniformly exhaustive if $\operatorname { lim } _ { n \rightarrow \infty } m _ { i } ( E _ { n } ) = 0$ uniformly in $i$ for each sequence $\{ E _ { n } \}$ of pairwise disjoint sets from the $\sigma$-algebra $\Sigma$. | ||
| − | + | Being a generalization of the [[Nikodým convergence theorem|Nikodým convergence theorem]], the Brooks–Jewett theorem [[#References|[a1]]] says that for a pointwise-convergent sequence $\{ m _ { n } \}$ of finitely additive scalar and exhaustive set functions (strongly additive) defined on a $\sigma$-algebra $\Sigma$, i.e. such that $\operatorname { lim } _ { n \rightarrow \infty } m _ { n } ( E ) = m ( E )$, $E \in \Sigma$: | |
| − | + | i) $m$ is an additive and exhaustive set function; | |
| − | + | ii) $\{ m _ { n } \}$ is uniformly exhaustive. | |
| − | + | There is a generalization of the Brooks–Jewett theorem for $k$-triangular set functions defined on algebras with some weak $\sigma$-conditions ($m : \Sigma \rightarrow [ 0 , \infty )$ is said to be $k$-triangular for $k \geq 1$ if $m ( \emptyset ) = 0$ and | |
| − | + | \begin{equation*} m ( A ) - k m ( B ) \leq m ( A \bigcup B ) \leq m ( A ) + k m ( B ) \end{equation*} | |
| − | + | whenever $A , B \in \Sigma$, $A \cap B = \emptyset$). The following definitions are often used [[#References|[a2]]], [[#References|[a6]]], [[#References|[a5]]]: | |
| − | + | SCP) An algebra $\mathcal{A}$ has the sequential completeness property if each disjoint sequence $\{ E _ { n } \}$ from $\mathcal{A}$ has a subsequence $\{ E _ { n_j} \}$ whose union is in $\mathcal{A}$. | |
| − | and | + | SIP) An algebra $\mathcal{A}$ has the subsequentional interpolation property if for each subsequence $\{ A _ { j n } \}$ of each disjoint sequence $\{ A _ { j } \}$ from $\mathcal{A}$ there are a subsequence $\{ A _ { j n _ { k } } \}$ and a set $B \in \mathcal{A}$ such that |
| − | + | <table class="eq" style="width:100%;"> <tr><td style="width:94%;text-align:center;" valign="top"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120490/b12049043.png"/></td> </tr></table> | |
| − | + | and $A _ { j } \cap B = \emptyset$ for $j \in \mathbf{N} \backslash \{ j _ { n_k } : k \in \mathbf{N} \}$. | |
| − | + | According to [[#References|[a5]]]: Let $\mathcal{A}$ satisfy SIP) and let $\{ m _ { n } \}$, $m _ { n } : {\cal A} \rightarrow [ 0 , + \infty )$, $n \in \mathbf N$, be a sequence of $k$-triangular exhaustive set functions. If the limit | |
| − | There are further generalizations of the Brooks–Jewett theorem, with respect to: the domain of the set functions (orthomodular lattices, | + | \begin{equation*} \operatorname { lim } _ { n \rightarrow \infty } m _ { n } ( E ) = m _ { 0 } ( E ) \end{equation*} |
| + | |||
| + | exists for each $E \in \mathcal{A}$ and $m_0$ is exhaustive, then $\{ m _ { n } \} _ { n = 0 } ^ { \infty }$ is uniformly exhaustive and $m_0$ is $k$-triangular. | ||
| + | |||
| + | There are further generalizations of the Brooks–Jewett theorem, with respect to: the domain of the set functions (orthomodular lattices, $D$-posets); properties of the set functions; and the range (topological groups, uniform semi-groups, uniform spaces), [[#References|[a2]]], [[#References|[a4]]], [[#References|[a5]]]. | ||
It is known that for additive set functions the Brooks–Jewett theorem is equivalent with the [[Nikodým convergence theorem|Nikodým convergence theorem]], and even more with the [[Vitali–Hahn–Saks theorem|Vitali–Hahn–Saks theorem]] [[#References|[a3]]]. | It is known that for additive set functions the Brooks–Jewett theorem is equivalent with the [[Nikodým convergence theorem|Nikodým convergence theorem]], and even more with the [[Vitali–Hahn–Saks theorem|Vitali–Hahn–Saks theorem]] [[#References|[a3]]]. | ||
| Line 34: | Line 42: | ||
====References==== | ====References==== | ||
| − | <table>< | + | <table><tr><td valign="top">[a1]</td> <td valign="top"> J. Brooks, R. Jewett, "On finitely additive vector measures" ''Proc. Nat. Acad. Sci. USA'' , '''67''' (1970) pp. 1294–1298</td></tr><tr><td valign="top">[a2]</td> <td valign="top"> C. Constantinescu, "Some properties of spaces of measures" ''Suppl. Atti Sem. Mat. Fis. Univ. Modena'' , '''35''' (1991) pp. 1–286</td></tr><tr><td valign="top">[a3]</td> <td valign="top"> L. Drewnowski, "Equivalence of Brooks–Jewett, Vitali–Hahn–Saks and Nikodým theorems" ''Bull. Acad. Polon. Sci.'' , '''20''' (1972) pp. 725–731</td></tr><tr><td valign="top">[a4]</td> <td valign="top"> A.B. D'Andrea, P. de Lucia, "The Brooks–Jewett theorem on an orthomodular lattice" ''J. Math. Anal. Appl.'' , '''154''' (1991) pp. 507–522</td></tr><tr><td valign="top">[a5]</td> <td valign="top"> E. Pap, "Null-additive set functions" , Kluwer Acad. Publ. &Ister Sci. (1995)</td></tr><tr><td valign="top">[a6]</td> <td valign="top"> H. Weber, "Compactness in spaces of group-valued contents, the Vitali–Hahn–Saks theorem and the Nikodym's boundedness theorem" ''Rocky Mtn. J. Math.'' , '''16''' (1986) pp. 253–275</td></tr></table> |
Revision as of 17:01, 1 July 2020
Let $X$ be a topological group. A set function $m : \Sigma \rightarrow X$ is exhaustive (also called strongly bounded) if $\operatorname { lim } _ { n \rightarrow \infty } m ( E _ { n } ) = 0$ for each sequence $\{ E _ { n } \}$ of pairwise disjoint sets from the $\sigma$-algebra $\Sigma$ (cf. also Measure). A sequence $\{ m_i \}$ of set functions $m _ { i } : \Sigma \rightarrow X$, $i \in \mathbf{N}$, is uniformly exhaustive if $\operatorname { lim } _ { n \rightarrow \infty } m _ { i } ( E _ { n } ) = 0$ uniformly in $i$ for each sequence $\{ E _ { n } \}$ of pairwise disjoint sets from the $\sigma$-algebra $\Sigma$.
Being a generalization of the Nikodým convergence theorem, the Brooks–Jewett theorem [a1] says that for a pointwise-convergent sequence $\{ m _ { n } \}$ of finitely additive scalar and exhaustive set functions (strongly additive) defined on a $\sigma$-algebra $\Sigma$, i.e. such that $\operatorname { lim } _ { n \rightarrow \infty } m _ { n } ( E ) = m ( E )$, $E \in \Sigma$:
i) $m$ is an additive and exhaustive set function;
ii) $\{ m _ { n } \}$ is uniformly exhaustive.
There is a generalization of the Brooks–Jewett theorem for $k$-triangular set functions defined on algebras with some weak $\sigma$-conditions ($m : \Sigma \rightarrow [ 0 , \infty )$ is said to be $k$-triangular for $k \geq 1$ if $m ( \emptyset ) = 0$ and
\begin{equation*} m ( A ) - k m ( B ) \leq m ( A \bigcup B ) \leq m ( A ) + k m ( B ) \end{equation*}
whenever $A , B \in \Sigma$, $A \cap B = \emptyset$). The following definitions are often used [a2], [a6], [a5]:
SCP) An algebra $\mathcal{A}$ has the sequential completeness property if each disjoint sequence $\{ E _ { n } \}$ from $\mathcal{A}$ has a subsequence $\{ E _ { n_j} \}$ whose union is in $\mathcal{A}$.
SIP) An algebra $\mathcal{A}$ has the subsequentional interpolation property if for each subsequence $\{ A _ { j n } \}$ of each disjoint sequence $\{ A _ { j } \}$ from $\mathcal{A}$ there are a subsequence $\{ A _ { j n _ { k } } \}$ and a set $B \in \mathcal{A}$ such that
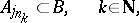 |
and $A _ { j } \cap B = \emptyset$ for $j \in \mathbf{N} \backslash \{ j _ { n_k } : k \in \mathbf{N} \}$.
According to [a5]: Let $\mathcal{A}$ satisfy SIP) and let $\{ m _ { n } \}$, $m _ { n } : {\cal A} \rightarrow [ 0 , + \infty )$, $n \in \mathbf N$, be a sequence of $k$-triangular exhaustive set functions. If the limit
\begin{equation*} \operatorname { lim } _ { n \rightarrow \infty } m _ { n } ( E ) = m _ { 0 } ( E ) \end{equation*}
exists for each $E \in \mathcal{A}$ and $m_0$ is exhaustive, then $\{ m _ { n } \} _ { n = 0 } ^ { \infty }$ is uniformly exhaustive and $m_0$ is $k$-triangular.
There are further generalizations of the Brooks–Jewett theorem, with respect to: the domain of the set functions (orthomodular lattices, $D$-posets); properties of the set functions; and the range (topological groups, uniform semi-groups, uniform spaces), [a2], [a4], [a5].
It is known that for additive set functions the Brooks–Jewett theorem is equivalent with the Nikodým convergence theorem, and even more with the Vitali–Hahn–Saks theorem [a3].
See also Diagonal theorem.
References
| [a1] | J. Brooks, R. Jewett, "On finitely additive vector measures" Proc. Nat. Acad. Sci. USA , 67 (1970) pp. 1294–1298 |
| [a2] | C. Constantinescu, "Some properties of spaces of measures" Suppl. Atti Sem. Mat. Fis. Univ. Modena , 35 (1991) pp. 1–286 |
| [a3] | L. Drewnowski, "Equivalence of Brooks–Jewett, Vitali–Hahn–Saks and Nikodým theorems" Bull. Acad. Polon. Sci. , 20 (1972) pp. 725–731 |
| [a4] | A.B. D'Andrea, P. de Lucia, "The Brooks–Jewett theorem on an orthomodular lattice" J. Math. Anal. Appl. , 154 (1991) pp. 507–522 |
| [a5] | E. Pap, "Null-additive set functions" , Kluwer Acad. Publ. &Ister Sci. (1995) |
| [a6] | H. Weber, "Compactness in spaces of group-valued contents, the Vitali–Hahn–Saks theorem and the Nikodym's boundedness theorem" Rocky Mtn. J. Math. , 16 (1986) pp. 253–275 |
Brooks-Jewett theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Brooks-Jewett_theorem&oldid=22193