Difference between revisions of "Bernstein-Bézier form"
Ulf Rehmann (talk | contribs) m (moved Bernstein–Bézier form to Bernstein-Bezier form: ascii title) |
Ulf Rehmann (talk | contribs) m (moved Bernstein-Bezier form to Bernstein-Bézier form: accented title) |
(No difference)
| |
Revision as of 07:54, 26 March 2012
Bernstein form, Bézier polynomial
The Bernstein polynomial of order  for a function
for a function 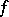 , defined on the closed interval
, defined on the closed interval 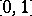 , is given by the formula
, is given by the formula
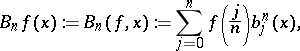 |
with
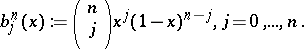 |
The polynomial was introduced in 1912 (see, e.g., [a3]) by S.N. Bernstein (S.N. Bernshtein) and shown to converge, uniformly on the interval 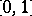 as
as 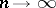 , to
, to 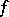 in case
in case 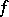 is continuous, thus providing a wonderfully short, probability-theory based, constructive proof of the Weierstrass approximation theorem (cf. Weierstrass theorem).
is continuous, thus providing a wonderfully short, probability-theory based, constructive proof of the Weierstrass approximation theorem (cf. Weierstrass theorem).
The Bernstein polynomial 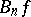 is of degree
is of degree 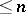 and agrees with
and agrees with 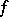 in case
in case 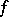 is a polynomial of degree
is a polynomial of degree 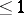 . It depends linearly on
. It depends linearly on 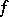 and is positive on
and is positive on  in case
in case 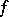 is positive there, and so has served as the starting point of the theory concerned with the approximation of continuous functions by positive linear operators (see, e.g., [a1] and Approximation of functions, linear methods), with the Bernstein operator,
is positive there, and so has served as the starting point of the theory concerned with the approximation of continuous functions by positive linear operators (see, e.g., [a1] and Approximation of functions, linear methods), with the Bernstein operator, 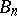 , the prime example. See also Bernstein polynomials.
, the prime example. See also Bernstein polynomials.
The 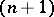 -sequence
-sequence 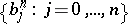 is evidently linearly independent, hence a basis for the
is evidently linearly independent, hence a basis for the 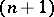 -dimensional linear space
-dimensional linear space 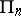 of all polynomials of degree
of all polynomials of degree 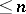 which contains it. It is called the Bernstein–Bézier basis, or just the Bernstein basis, and the corresponding representation
which contains it. It is called the Bernstein–Bézier basis, or just the Bernstein basis, and the corresponding representation
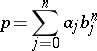 |
is called the Bernstein–Bézier form, or just the Bernstein form, for 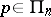 . Thanks to the fundamental work of P. Bézier and P. de Casteljau, this form has become the standard way in computer-aided geometric design (see, e.g., [a2]) for representing a polynomial curve, that is, the image
. Thanks to the fundamental work of P. Bézier and P. de Casteljau, this form has become the standard way in computer-aided geometric design (see, e.g., [a2]) for representing a polynomial curve, that is, the image  of the interval
of the interval 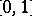 under a vector-valued polynomial
under a vector-valued polynomial 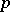 . The coefficients
. The coefficients 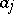 in that form readily provide information about the value of
in that form readily provide information about the value of  and its derivatives at both endpoints of the interval
and its derivatives at both endpoints of the interval 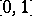 , hence facilitate the concatenation of polynomial curve pieces into a more or less smooth curve.
, hence facilitate the concatenation of polynomial curve pieces into a more or less smooth curve.
Somewhat confusingly, the term "Bernstein polynomial" is at times applied to the polynomial 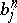 , the term "Bézier polynomial" is often used to refer to the Bernstein–Bézier form of a polynomial, and, in the same vein, the term "Bézier curve" is often used for a curve that is representable by a polynomial, as well as for the Bernstein–Bézier form of such a representation.
, the term "Bézier polynomial" is often used to refer to the Bernstein–Bézier form of a polynomial, and, in the same vein, the term "Bézier curve" is often used for a curve that is representable by a polynomial, as well as for the Bernstein–Bézier form of such a representation.
References
| [a1] | R.A. DeVore, "The approximation of continuous functions by positive linear operators" , Springer (1972) |
| [a2] | G. Farin, "Curves and surfaces for computer aided geometric design" , Acad. Press (1993) (Edition: Third) |
| [a3] | G.G. Lorentz, "Bernstein polynomials" , Univ. Toronto Press (1953) |
Bernstein-Bézier form. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Bernstein-B%C3%A9zier_form&oldid=22101