Difference between revisions of "Convergence of measures"
(MSC|28A33 Category:Classical measure theory (again)) |
Ulf Rehmann (talk | contribs) m (Undo revision 20869 by Boris Tsirelson (talk)) |
||
| Line 1: | Line 1: | ||
| + | {{MSC|28A33}} | ||
| + | A concept in measure theory, determined by a certain topology in a space of measures that are defined on a certain <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c026/c026140/c0261401.png" />-algebra <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c026/c026140/c0261402.png" /> of subsets of a space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c026/c026140/c0261403.png" /> or, more generally, in a space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c026/c026140/c0261404.png" /> of charges, i.e. countably-additive real or complex functions <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c026/c026140/c0261405.png" />, defined on sets from <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c026/c026140/c0261406.png" />. The following are the most commonly used topologies in the subspace <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c026/c026140/c0261407.png" /> consisting of bounded charges, i.e. charges for which <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c026/c026140/c0261408.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c026/c026140/c0261409.png" />. | ||
| + | |||
| + | 1) In <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c026/c026140/c02614010.png" /> the norm | ||
| + | |||
| + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c026/c026140/c02614011.png" /></td> </tr></table> | ||
| + | |||
| + | called the variation of the charge <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c026/c026140/c02614012.png" />, is introduced. The convergence of a sequence of charges <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c026/c026140/c02614013.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c026/c026140/c02614014.png" />, to a charge <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c026/c026140/c02614015.png" /> in this norm is called convergence in variation. | ||
| + | |||
| + | 2) In <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c026/c026140/c02614016.png" /> the ordinary weak topology is examined: Convergence of a sequence of charges <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c026/c026140/c02614017.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c026/c026140/c02614018.png" />, in this topology (weak convergence) means that for any continuous linear function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c026/c026140/c02614019.png" /> on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c026/c026140/c02614020.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c026/c026140/c02614021.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c026/c026140/c02614022.png" />. This convergence is equivalent to the fact that the sequence of charges is bounded, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c026/c026140/c02614023.png" />, and that for any set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c026/c026140/c02614024.png" /> the sequence of values <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c026/c026140/c02614025.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c026/c026140/c02614026.png" />. Weak convergence of a sequence of charges <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c026/c026140/c02614027.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c026/c026140/c02614028.png" /> implies convergence of the integrals <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c026/c026140/c02614029.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c026/c026140/c02614030.png" />, for any bounded function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c026/c026140/c02614031.png" /> on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c026/c026140/c02614032.png" /> that is measurable with respect to the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c026/c026140/c02614033.png" />-algebra <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c026/c026140/c02614034.png" />. | ||
| + | |||
| + | 3) When <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c026/c026140/c02614035.png" /> is a topological space and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c026/c026140/c02614036.png" /> is its Borel <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c026/c026140/c02614037.png" />-algebra, a topology is examined in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c026/c026140/c02614038.png" /> which is also called the weak topology (or sometimes the narrow topology). It is defined as the weakest of the topologies in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c026/c026140/c02614039.png" /> relative to which all functionals of the form | ||
| + | |||
| + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c026/c026140/c02614040.png" /></td> </tr></table> | ||
| + | |||
| + | are continuous, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c026/c026140/c02614041.png" /> is an arbitrary bounded continuous function on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c026/c026140/c02614042.png" />. This topology is weaker than the previous one, and convergence of a sequence of charges <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c026/c026140/c02614043.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c026/c026140/c02614044.png" />, relative to it (weak or narrow convergence) is equivalent to the convergence of the values <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c026/c026140/c02614045.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c026/c026140/c02614046.png" />, for any Borel set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c026/c026140/c02614047.png" /> for which <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c026/c026140/c02614048.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c026/c026140/c02614049.png" /> and the operation of closure of a set is denoted by the bar. | ||
| + | |||
| + | 4) When <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c026/c026140/c02614050.png" /> is a locally compact topological space (and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c026/c026140/c02614051.png" /> is a Borel <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c026/c026140/c02614052.png" />-algebra) in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c026/c026140/c02614053.png" /> the so-called wide topology is examined: the convergence of a sequence of charges <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c026/c026140/c02614054.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c026/c026140/c02614055.png" /> (wide convergence), means convergence of the functionals <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c026/c026140/c02614056.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c026/c026140/c02614057.png" />, for any continuous function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c026/c026140/c02614058.png" /> with compact support. This topology is weaker than the weak topology in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c026/c026140/c02614059.png" />. An analogous topology is defined naturally in the wider space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c026/c026140/c02614060.png" /> of locally bounded charges <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c026/c026140/c02614061.png" />, i.e. charges such that for any point <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c026/c026140/c02614062.png" /> there is a neighbourhood <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c026/c026140/c02614063.png" /> in which <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c026/c026140/c02614064.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c026/c026140/c02614065.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c026/c026140/c02614066.png" />. | ||
| + | |||
| + | ====References==== | ||
| + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> N. Bourbaki, "Elements of mathematics. Integration" , Addison-Wesley (1975) pp. Chapt.6;7;8 (Translated from French)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> N. Dunford, J.T. Schwartz, "Linear operators. General theory" , '''1''' , Interscience (1958)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> P. Billingsley, "Convergence of probability measures" , Wiley (1968)</TD></TR></table> | ||
Revision as of 17:53, 7 February 2012
2020 Mathematics Subject Classification: Primary: 28A33 [MSN][ZBL]
A concept in measure theory, determined by a certain topology in a space of measures that are defined on a certain  -algebra
-algebra  of subsets of a space
of subsets of a space  or, more generally, in a space
or, more generally, in a space  of charges, i.e. countably-additive real or complex functions
of charges, i.e. countably-additive real or complex functions  , defined on sets from
, defined on sets from 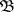 . The following are the most commonly used topologies in the subspace
. The following are the most commonly used topologies in the subspace  consisting of bounded charges, i.e. charges for which
consisting of bounded charges, i.e. charges for which  ,
,  .
.
1) In  the norm
the norm
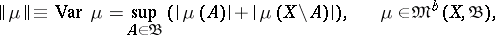 |
called the variation of the charge 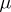 , is introduced. The convergence of a sequence of charges
, is introduced. The convergence of a sequence of charges  ,
,  , to a charge
, to a charge 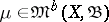 in this norm is called convergence in variation.
in this norm is called convergence in variation.
2) In  the ordinary weak topology is examined: Convergence of a sequence of charges
the ordinary weak topology is examined: Convergence of a sequence of charges 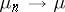 ,
, 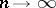 , in this topology (weak convergence) means that for any continuous linear function
, in this topology (weak convergence) means that for any continuous linear function 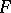 on
on 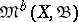 ,
, 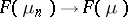 ,
, 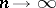 . This convergence is equivalent to the fact that the sequence of charges is bounded,
. This convergence is equivalent to the fact that the sequence of charges is bounded,  , and that for any set
, and that for any set 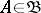 the sequence of values
the sequence of values 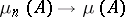 ,
, 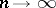 . Weak convergence of a sequence of charges
. Weak convergence of a sequence of charges  ,
, 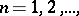 implies convergence of the integrals
implies convergence of the integrals  ,
,  , for any bounded function
, for any bounded function 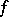 on
on  that is measurable with respect to the
that is measurable with respect to the 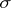 -algebra
-algebra 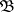 .
.
3) When  is a topological space and
is a topological space and  is its Borel
is its Borel  -algebra, a topology is examined in
-algebra, a topology is examined in 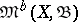 which is also called the weak topology (or sometimes the narrow topology). It is defined as the weakest of the topologies in
which is also called the weak topology (or sometimes the narrow topology). It is defined as the weakest of the topologies in 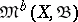 relative to which all functionals of the form
relative to which all functionals of the form
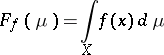 |
are continuous, where 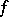 is an arbitrary bounded continuous function on
is an arbitrary bounded continuous function on  . This topology is weaker than the previous one, and convergence of a sequence of charges
. This topology is weaker than the previous one, and convergence of a sequence of charges  ,
,  , relative to it (weak or narrow convergence) is equivalent to the convergence of the values
, relative to it (weak or narrow convergence) is equivalent to the convergence of the values 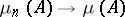 ,
, 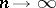 , for any Borel set
, for any Borel set 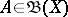 for which
for which 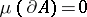 , where
, where 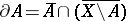 and the operation of closure of a set is denoted by the bar.
and the operation of closure of a set is denoted by the bar.
4) When  is a locally compact topological space (and
is a locally compact topological space (and 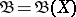 is a Borel
is a Borel 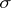 -algebra) in
-algebra) in  the so-called wide topology is examined: the convergence of a sequence of charges
the so-called wide topology is examined: the convergence of a sequence of charges 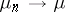 ,
, 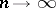 (wide convergence), means convergence of the functionals
(wide convergence), means convergence of the functionals  ,
, 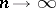 , for any continuous function
, for any continuous function 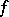 with compact support. This topology is weaker than the weak topology in
with compact support. This topology is weaker than the weak topology in 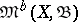 . An analogous topology is defined naturally in the wider space
. An analogous topology is defined naturally in the wider space 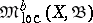 of locally bounded charges
of locally bounded charges 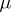 , i.e. charges such that for any point
, i.e. charges such that for any point  there is a neighbourhood
there is a neighbourhood  in which
in which  ,
, 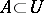 ,
, 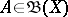 .
.
References
| [1] | N. Bourbaki, "Elements of mathematics. Integration" , Addison-Wesley (1975) pp. Chapt.6;7;8 (Translated from French) |
| [2] | N. Dunford, J.T. Schwartz, "Linear operators. General theory" , 1 , Interscience (1958) |
| [3] | P. Billingsley, "Convergence of probability measures" , Wiley (1968) |
Convergence of measures. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Convergence_of_measures&oldid=20869